Rumus Trapesium Luas, Keliling, Beserta Contoh Soal dan Pembahasan
Rumus Trapesium - Perhatikan denah rumah di bawah ini.
Perhatikan gambar-gambar di bawah ini.
Gambar di atas merupakan contoh-contoh gambar trapesium. Dari gambar di atas, bisa kita amati bahwa pada bentuk trapesium terdapat tepat sepasang sisi yang saling sejajar. Dari hal tersebut, maka trapesium dapat didefinisikan sebagai berikut.
Pada contoh gambar di atas diketahui bahwa trapesium (a) memiliki sepasang sisi yang berhadapan dan saling sejajar yaitu sisi AB dan sisi DC (dituliskan AB // DC). Sedangkan pada trapesium (b), dua sisi yang berhadapan dan saling sejajar itu adalah sisi EF dan sisi HG (ditulis EF // HG).
 |
| indochinatown |
Daftar Isi
Gambar denah di atas merupakan contoh bangun trapesium. Namun, tahukah kalian apa itu trapesium? Bagaimana sifat-sifat trapesium? Bagaimana cara untuk menentukan keliling dan luas trapesium? Untuk menjawab semua pertanyaan tersebut. Pelajarilah materi berikut dengan cermat.A. Pengertian Trapesium
Perhatikan gambar-gambar di bawah ini.
Gambar di atas merupakan contoh-contoh gambar trapesium. Dari gambar di atas, bisa kita amati bahwa pada bentuk trapesium terdapat tepat sepasang sisi yang saling sejajar. Dari hal tersebut, maka trapesium dapat didefinisikan sebagai berikut.
Trapesium adalah sebuah bangun datar dua dimensi yang di bentuk oleh empat buah rusuk yang dua di antaranya saling sejajar namun tidak sama panjang..
Pada contoh gambar di atas diketahui bahwa trapesium (a) memiliki sepasang sisi yang berhadapan dan saling sejajar yaitu sisi AB dan sisi DC (dituliskan AB // DC). Sedangkan pada trapesium (b), dua sisi yang berhadapan dan saling sejajar itu adalah sisi EF dan sisi HG (ditulis EF // HG).
B. Rumus Trapesium
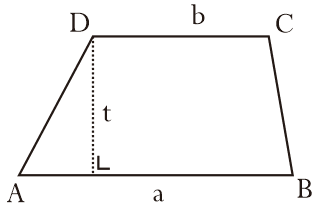
Keterangan gambar:
t = tinggi trapesium
a, b = adalah sisi yang sejajar, sisi a merupakan panjang AB dan sisi b merupakan panjang DC
| Nama | Rumus |
|---|---|
| Luas (L) | L=12×(a+b)×t L=(a+b)×t2 |
| Keliling (K) | K = AB + BC + CD + DA |
| Tinggi (t) | t=2×L(a+b) |
| Sisi a (CD) | a=2×Lt−b atau CD = K - AB - BC - AD |
| Sisi b (AB) | b=2×Lt−a atau AB = K - CD - BC - AD |
| Sisi AD | AD = K - CD - BC - AB |
| Sisi BC | BC = K - CD - AD - AB |
Keliling dan Luas Trapesium
Trapesium merupakan salah satu bangun datar. Setiap bangun datar pasti memiliki keliling dan luas, termasuk bangun trapesium. Berikut akan dijelaskan bagaimana cara untuk menentukan keliling dan luas dari bangun trapesium.
C. Rumus Keliling Trapesium
Keliling sebuah bangun datar dapat diartikan sebagai hasil jumlah dari semua panjang sisi bangun tersebut. Berikut akan dijelaskan cara menentukan keliling dari sebuah trapesium.
1. Menentukan Keliling Trapesium Siku-Siku
Misalkan dipunyai trapesium siku siku ABCD sebagai berikut.
Untuk menentukan keliling trapesium tersebut dapat digunakan rumus berikut ini.
Keliling Trapesium Siku-siku ABCD =AB+BC+CD+AD
Contoh Soal 1:
Dipunyai sebuah trapesium ABCD berikut.
Tentukan keliling trapesium di atas !
Jawab:
Untuk menentukan keliling bangun trapesium digunakan rumus:
K = AB + BC + CD + AD
= 8 + 5 + 5 + 4
= 22
Jadi, keliling trapesium ABCD adalah 22 cm.
2. Menentukan Keliling Trapesium Sama Kaki
Dipunyai sebuah trapesium sama kaki ABCD sebagai berikut.
Untuk menentukan keliling trapesium tersebut dapat digunakan rumus berikut.
Keliling Trapesium Sama Kaki ABCD =AB+BC+CD+AD
Contoh Soal 2:
Diketahui sebuah trapesium ABCD yang digambarkan sebagai berikut.
Tentukan keliling trapesium di atas !
Jawab:
Untuk menentukan keliling trapesium, maka kita harus mengetahui terlebih dahulu semua panjang sisi trapesium. Karena trapesium di atas adalah trapesium sama kaki, maka trapesium tersebut dapat digambarkan sebagai berikut.
Dengan demikian didapati:
AB = 3 cm + 6 cm + 3 cm = 12 cm;
BC = 5 cm;
CD = 6 cm;
AD = BC = 5 cm.
K = AB + BC + CD + AD
= 12 + 5 + 6 + 5
= 28
Jadi, keliling trapesium ABCD adalah 28 cm.
3. Menentukan Keliling Trapesium Sembarang
Misal dipunyai sebuah trapesium sembarang ABCD sebagai berikut.
Untuk menentukan keliling trapesium tersebut dapat digunakan rumus berikut.
Keliling Trapesium Tak Beraturan ABCD =AB+BC+CD+AD
Contoh Soal 3:
Diketahui sebuah trapesium ABCD yang digambarkan sebagai berikut.
Tentukan keliling trapesium di atas !
Jawab:
Untuk menentukan keliling trapesium digunakan rumus berikut ini:
K = AB + BC + CD + AD
= 16 + 10 + 5 + 7
= 38
Jadi, keliling trapesium ABCD adalah 38 cm.
D. Rumus Luas Trapesium
Luas daerah trapesium sama dengan setengah dari hasil kali antara tinggi t dan jumlah panjang sisi yang saling sejajar yaitu panjang sisi atas a dan panjang sisi bawah b. Berikut ini akan disajikan cara untuk menentukan luas daerah dari suatu bangun trapesium.
1. Menentukan Luas Trapesium Siku-Siku
Sebuah trapesium siku siku ABCD digambarkan sebagai berikut.
Untuk menentukan luas daerah trapesium di atas dapat digunakan rumus berikut ini.
Luas Trapesium Siku siku = 1/2 x t x (a+b)
Contoh Soal 4:
Dipunyai sebuah trapesium ABCD berikut.
Tentukan luas trapesium di atas !
Jawab:
Dari gambar di atas, didapati:
a = 5 cm;
b = 8 cm;
t = 4 cm.
Untuk menentukan luas bangun trapesium digunakan rumus:
L = 1/2 t ×(a+b)
= 1/2 (4) ×(5+8)
= 2 ×13
= 26
Jadi, luas daerah trapesium ABCD adalah 26 cm2.
2. Menentukan Luas Trapesium Sama Kaki
Diketahui sebuah trapesium sama kaki ABCD mempunyai ukuran sebagai berikut.
Untuk menentukan luas daerah trapesium tersebut dapat digunakan rumus berikut.
Luas Trapesium Sama Kaki = 1/2 x t x (a+b)
Contoh Soal 5:
Dipunyai sebuah trapesium sama kaki ABCD berikut.
Tentukan luas trapesium tersebut !
Jawab:
Dari gambar di atas, didapati:
a = 5 cm;
b = 11 cm;
t = 4 cm.
Untuk menentukan luas daerah trapesium digunakan rumus:
L = 1/2 t ×(a+b)
= 1/2 (4) ×(5+11)
= 2 ×16
= 32
Jadi, luas daerah trapesium ABCD adalah 32 cm2.
3. Menentukan Luas Trapesium Sembarang
Dipunyai sebuah trapesium sembarang ABCD yang digambarkan sebagai berikut.
Untuk menentukan luas daerah trapesium dapat digunakan rumus berikut.
Luas Trapesium Sembarang = 1/2 x t x (a+b)
Contoh Soal 6:
Sebuah trapesium sembarang diketahui mempunyai panjang sisi-sisi yang sejajar masing-masing adalah 12 cm dan 24 cm. Jika tinggi trapesium tersebut adalah 16 cm, hitunglah berapa luas daerah trapesium tersebut!
Jawab:
Dari contoh soal 6 didapati informasi yaitu:
Misalkan
a = 12 cm;
b = 24 cm;
t = 16 cm.
Untuk menentukan luas daerah trapesium digunakan rumus:
L = 1/2 t ×(a+b)
= 1/2 (16) ×(12+24)
= 8 ×36
= 288
Jadi, luas daerah trapesium sembarang tersebut adalah 288 cm2.
E. Jenis-jenis Trapesium
Perhatikan kembali gambar trapesium (a) dan (b) pada materi Pengertian Trapesium. Dari gambar tersebut, dapat diketahui bahwa trapesium memiliki bentuk yang beragam.
Berdasarkan jenisnya, trapesium dapat dibedakan menjadi tiga jenis trapesium yaitu trapesium siku-siku, trapesium sama kaki, dan trapesium sembarang.
Perhatikan gambar trapesium di atas. Sebuah trapesium siku-siku memiliki beberapa sifat yang membedakannya dengan trapesium-trapesium lainnya.
Sifat-sifat tersebut antara lain:
Trapesium sama kaki di atas memiliki beberapa sifat yang membedakannya dengan trapesium lainnya antara lain sebagai berikut.
Trapesium sembarang seperti gambar di atas memiliki beberapa sifat antara lain sebagai berikut.
1. Trapesium Siku-Siku
Trapesium Siku-Siku adalah trapesium yang salah satu sudutnya berbentuk siku-siku. Dengan kata lain, salah satu sudutnya memiliki besar 90o. Berikut adalah contoh trapesium siku-siku ABCD dengan sudut siku-siku di A.Perhatikan gambar trapesium di atas. Sebuah trapesium siku-siku memiliki beberapa sifat yang membedakannya dengan trapesium-trapesium lainnya.
Sifat-sifat tersebut antara lain:
- Memiliki tepat sepasang sisi berhadapan yang saling sejajar.
- Memiliki dua buah sudut siku-siku yang posisinya saling berdekatan.
- Memiliki diagonal dengan panjang yang berbeda.
2. Trapesium Sama Kaki
Trapesium Sama Kaki adalah trapesium yang memiliki sepasang sisi dengan panjang yang sama. Berikut ini adalah contoh gambar trapesium sama kaki ABCD.Trapesium sama kaki di atas memiliki beberapa sifat yang membedakannya dengan trapesium lainnya antara lain sebagai berikut.
- Memiliki dua sisi dengan panjang yang sama dan dua sisi yang sejajar memiliki panjang yang berbeda.
- Dua sudut yang berdekatan memiliki besar yang sama.
- Memiliki dua diagonal dengan panjang yang sama.
3. Trapesium Sembarang
Trapesium sembarang adalah trapesium yang keempat sisinya memiliki panjang yang berbeda. Di bawah ini adalah contoh trapesium sembarang EFGH.Trapesium sembarang seperti gambar di atas memiliki beberapa sifat antara lain sebagai berikut.
- Memiliki empat sisi dengan panjang yang berbeda.
- Keempat sudutnya memiliki besar yang tidak sama.
- Memiliki dua diagonal dengan panjang yang berbeda.
Demikian sekilas pembahasan tentang rumus trapesium, Jika da pertanyaan atau komentar kamu bisa tulis di kolom komentar. Semoga bermanfaat….[resky]