Sifat-Sifat Segitiga Siku Siku dan Contoh Soalnya
Segitiga siku-siku merupakan salah satu jenis segitiga dilihat dari besar sudutnya. Segitiga jenis ini sangat mudah untuk di pahami ciri dan sifatnya. Berikut adalah beberapa sifat atau ciri segitiga ssiku-siku.
Segitiga siku-siku bisa terbentuk dari sebuah bangun persegi panjang, yaitu dengan cara menarik salah satu garis diagonal pada persegi panjang.
Ketika garis diagonal sudah terhubung maka akan terbentuklah dua buah segitiga siku siku yang sama besar dan sebangun atau kongruen.
Sebuah segitiga siku-siku memliki dua buah sisi siku-siku, yang dimana kedua sisi siku-siku tersebut mengapit sebuah sudut siku-siku dan 1 sisi miring atau hypotenusa.
Baca juga pembahasan rumus segitiga siku-siku.
Itulah beberapa ciri atau sifat segitiga siku-siku semoga bermanfaat.[]
Segitiga siku-siku bisa terbentuk dari sebuah bangun persegi panjang, yaitu dengan cara menarik salah satu garis diagonal pada persegi panjang.
Ketika garis diagonal sudah terhubung maka akan terbentuklah dua buah segitiga siku siku yang sama besar dan sebangun atau kongruen.
Sebuah segitiga siku-siku memliki dua buah sisi siku-siku, yang dimana kedua sisi siku-siku tersebut mengapit sebuah sudut siku-siku dan 1 sisi miring atau hypotenusa.
Baca juga pembahasan rumus segitiga siku-siku.
Sifat Segitiga Siku Siku
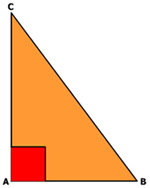
Perhatikan gambar segitiga ABC di atas, dari gambar tersebut kita bisa melihat jika segitiga siku-siku mempunyai ciri-ciri:- Segitiga siku-siku memiliki dua buah sisi siku-siku, yang dimana kedua sisi siku-siku tersebut mengapit sebuah sudut siku-siku dan 1 sisi miring atau hypotenusa.
- Memiliki 2 sisi yang saling tegak lurus.
- Hypotenusa atau sisi miring di setiap segitiga siku-siku selalu terletak di depan sudut siku-siku.
- Memiliki satu buah sudut yang besarnya 90 derajat.
- Tidak memiliki simetri putar.
- Segitiga siku siku sama kaki memiliki 1 simetri lipat.
- Jumlah kedua sudut selain sudut siku siku adalah 90 derajat.
- Berlaku teorema phytagoras.
Contoh Soal
Diketahui sudut C = 40 derajat, panjang AC = 4 cm, panjang AB = 3 cm.

Tentukan:
a) luas segitiga siku-siku
b) Panjang sisi BC
c) keliling segitiga siku-siku
d) besar sudut B
Jawab :
a) Luas = 1/2 x alas x tinggi
L = 1/2 x 3 x 4
L = 6 cm2
b) Panjang sisi BC
Dalam segitiga siku siku berlaku teorema pythagoras yaitu: kuadrat sisi miring = jumlah kuadrat seluruh sisi siku-siku
BC2 = AC2 + AB2
BC2 = 42 + 32
BC2 = 16 + 9
BC2 = 25
BC = akar 25
BC = 5 cm
c) Keliling segitiga = jumlah sisi segitiga
K = 4 cm + 3 cm + 5 cm
K = 12 cm
d) Besar sudut B….? sudut A = 90 derajat dan sudut C = 40 derajat
sebuah segitiga memiliki jumlah seluruh sudut adalah 180 derajat, maka:
sudut B = 180 – (90 + 40)
sudut B = 50 derajat
