8 Macam Bangun Ruang | Pengertian, Rumus, Volume, Luas, dan Gambar
Pengertian Bangun Ruang
Bangun ruang merupakan penamaan atau sebutan untuk bangun-bangun tiga dimensi atau bangun yang mempunyai ruang yang dibatasi oleh sisi-sisinya.
Contoh bangun ruang antara lain kubus, balok, prisma, tabung, kerucut, limas dan bola. Berikut ini macam-macam bangun ruang :
1. Kubus
Kubus adalah bangun ruang yang mempunyai panjang rusuk yang sama atau bangun yang di batasi oleh enam buah sisi yang sama dan sebangun, serta merupakan bangun ruang tiga dimensi. Lebih lengkapnya silahkan baca di Rumus Bangun Ruang Kubus.
| Nama | Rumus |
|---|---|
| Volume (V) | V = s × s × s |
| V = s3 | |
| Luas permukaan (L) | L = 6 × s × s |
| L = 6 × s2 | |
| Sisi rusuk (s) | S = $\sqrt[3]{V}$ |
| S = $\sqrt{\frac{L}{6}}$ | |
| Diagonal sisi (ds) | ds = S$\sqrt{2}$ |
| Diagonal ruang (dr) | dr = S$\sqrt{3}$ |
| Luas bidang diagonal (bd) | bd = S2$\sqrt{2}$ |
Keterangan:
s = panjang sisi kubus
Ciri Ciri Kubus
1. Jumlah bidang sisinya ada enam buah yang semuanya berbentuk bujur sangkar.2. Memiliki delapan buah titik sudut.
3. Memiliki 12 rusuk yang sama panjang.
4. Semua sudutnya siku-siku.
5. Memiliki 4 diagonal ruang dan 12 diagonal bidang.
2. Balok
Balok merupakan bangun ruang tiga dimensi yang terbentuk oleh enam buah persegi panjang yang saling tegak lurus. Contoh bangun ruang balok sering kita dapati dalam kehidupan kita sehari-hari yaitu lemari es dan lemari pakaian. Lebih lengkapnya silahkan baca di Rumus Bangun Ruang Balok.
| Nama | Rumus |
|---|---|
| Volume (V) | V = p × l × t |
| Luas Permukaan (L) | L = 2 × (p.l + p.t +l.t) |
| Panjang (p) | p = V : (l x t) (Jika diketahui Volume) |
| p = $\frac {\frac {L}{2}-(l \times t)}{l+t}$ (jika diketahui luas permukaan) | |
| Lebar (l) | l = V ÷ (p x t) (Jika diketahui Volume) |
| l = $\frac {\frac {L}{2}-(p \times t)}{p+t}$ (jika diketahui luas permukaan) | |
| Tinggi (t) | t = V ÷ (p x l) (Jika diketahui Volume) |
| t = $\frac {\frac {L}{2}-(p \times l)}{p+l}$ (jika diketahui luas permukaan) | |
| Diagonal bidang atau sisi (ds) | db1 = $\sqrt{p^{2}+l^{2}}$ db2 = $\sqrt{p^{2}+t^{2}}$ db3 = $\sqrt{l^{2}+t^{2}}$ |
| Diagonal ruang (dr) | dr = $\sqrt{(p^{2}+l^{2}+t^{2})}$ |
| Luas bidang diagonal (bd) | bd1 = db1 x t bd2 = db2 x l bd3 = db3 x p |
Keterangan:
t = tinggi
p = panjang
l = lebar
Ciri Ciri Balok
1. Memiliki 4 buah sisi berbentuk persegi panjang dan 2 buah sisi yang memiliki bentuk sama.2. Terdiri dari dua belas rusuk.
3. Memiliki enam bidang sisi.
4. Memiliki delapan titik sudut.
5. Seluruh sudutnya siku-siku.
6. Mempunyai 4 diagonal ruang dan 12 diagonal bidang.
3. Prisma
Prisma merupakan bangun ruang tiga dimensi yang mempunyai alas dan atap yang berbentuk segi-n dengan ukuran yang sama atau kongruen dan sisi tegaknya berupa segiempat atau persegi panjang. Selengkapnya baca di Rumus Prisma.
| Nama | Rumus |
|---|---|
| Volume (V) | V = Luas alas × t |
| tinggi (t) jika diketahui V | t = V ÷ Luas Alas |
| Luas Permukaan (L) | L = t × ( a1 + a2 + ... + an) + (2 × La) |
| L = t × (Keliling Alas) + (2 × La) | |
| ∴ Luas Prisma Segi-3 | L = t × ( a1 + a2 + a3) + (2 × La) |
| ∴ Luas Prisma Segi-4 | L = t × ( a1 + a2 + a3 + a4) + (2 × La) |
| ∴ Luas Prisma Segi-5 | L = t × ( a1 + a2 + a3 + a4 + a5) + (2 × La) |
| ∴ Luas Prisma Segi-6 | L = t × ( a1 + a2 + a3 + a4 + a5 + a6) + (2 × La) |
| Luas Alas (La) | tergantung bentuk alas prisma |
Keterangan:
t = tinggi prisma
La = luas alas
Ciri-Ciri Prisma
1. Bentuk alas dan atap prisma bersifat kongruen (sama dan sebangun).2. Alas dan atap prisma memiliki bentuk segi-n, misalnya segitiga.
3. Semua bidang sisi tegak prisma berbentuk segi empat atau persegi panjang.
4. Jumlah semua sisi prisma adalah n+2, contoh:
- Prisma segitiga = n+2 = 3+2 = 5 buah sisi
- Prisma segi empat = n+2 = 4+2 = 6 buah sisi
- Prisma segi lima = n+2 = 5+2 = 7 buah sisi
- Prisma segi enam = n+2 = 6+2 = 8 buah sisi
- Prisma segitiga = 3xn = 3x3 = 9 buah rusuk
- Prisma segi empat = 3xn = 3x4 = 12 buah rusuk
- Prisma segi lima = 3xn = 3x5 = 15 buah rusuk
- Prisma segi enam = 3xn = 3x6 = 18 buah rusuk
- Prisma segitiga = 2xn = 2×3 = 6 buah titik sudut
- Prisma segi empat = 2xn = 2×4 = 8 buah titik sudut
- Prisma segi lima = 2xn = 2×5 = 10 buah titik sudut
- Prisma segi enam = 2xn = 2×6 = 12 buah titik sudut
4. Limas
Limas merupakan sebuah bangun ruang yang mempunyai alas segi n dan sisi tegaknya juga berupa segitiga Lebih jelasnya silahkan baca di Rumus Limas Segitiga dan Limas Segiempat.
4.1 Limas Segitiga
Limas segitiga adalah bangun ruang yang memiliki alas berbentuk segitiga dengan sisi tegaknya juga berbentuk segitiga.
Keterangan:
t = tinggi limas (PO)
as = panjang segitiga alas limas (AB)
ts = tinggi segitiga alas limas (DC)
t1, t2, t3 = tinggi masing-masing bidang tegak
a1, a2, a3 = alas masing-masing bidang tegak
| Nama | Rumus |
|---|---|
| Volume (V) | V = ⅓ × La × t |
| Luas Alas (La) | La = ½ × a × t |
| Luas Permukaan (L) | L = L alas + L ΔI + L ΔII + L ΔIII |
| Tinggi (t) | t = $\frac {3 \times V}{La}$ |
| Alas segitiga alas (as) | as = $\frac {6 \times V}{ts \times t}$ |
| Tinggi segitiga alas (ts) | ts = $\frac {6 \times V}{as \times t}$ |
| Luas ΔI | L ΔI = ½ × a Δ1 × t Δ1 |
| Luas ΔII | L ΔII = ½ × a Δ2 × t Δ2 |
| Luas ΔIII | L ΔIII = ½ × a Δ3 × t Δ3 |
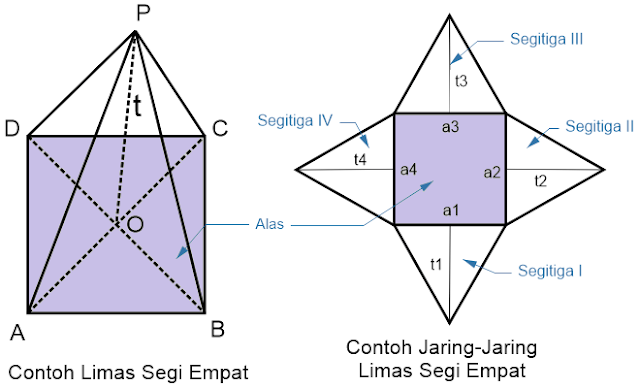
4.2 Limas Segiempat
Limas segiempat merupakan salah satu bangun ruang (3 dimensi) yang mempunyai lima sisi dengan alasnya yang berbentuk segi empat dan sisi tegaknya berbentuk segitiga.
Rumus Limas Segi Empat
| Nama | Rumus |
|---|---|
| Volume (V) | V = ⅓ × L alas × t |
| Luas Permukaan (L) | L = L alas + L ΔI + L ΔII + L ΔIII + L ΔIV |
| Tinggi | t = $\frac {3 \times V}{La}$ |
Luas Alas Limas Segi Empat
| Jenis Alas | Luas Alas (La) |
|---|---|
| Alas Persegi | La = s × s |
| Alas Persegi Panjang | La = p × l |
| Alas Jajar Genjang | La = a × t |
| Alas Trapesium | L = $\frac {1}{2} \times (a + b) \times t $ L = $\frac {(a + b) \times t}{2}$ |
| Alas Belah Ketupat | La = ½ × d1 × d2 |
| Alas Layang-Layang | La = ½ × d1 × d2 |
Luas Sisi Tegak Limas Segi Empat
| Sisi Tegak | Luas |
|---|---|
| Luas ΔI | L ΔI = ½ × a Δ1 × t Δ1 |
| Luas ΔII | L ΔII = ½ × a Δ2 × t Δ2 |
| Luas ΔIII | L ΔIII = ½ × a Δ3 × t Δ3 |
| Luas ΔIV | L ΔIII = ½ × a Δ4 × t Δ4 |
5. Tabung
Tabung merupakan bangun ruang yang dibatasi sisi lengkung dan dua buah lingkaran, atau dalam pengertian lain Tabung merupakan sebuah bangun ruang tiga dimensi yang memiliki tutup dan alas yang berbentuk lingkaran dengan ukuran yang sama dengan bagian selimutnya berbentuk persegi panjang. Untuk selengkapnya baca Volume Tabung.
| Nama | Rumus |
|---|---|
| Volume (V) | V = π × r × r × t |
| V = π × r² × t | |
| Luas Permukaan (L) | L = 2 × π × r × (r + t) |
| Luas Selimut (Ls) | Ls = 2 × π × r × t |
| Ls = π × d × t | |
| Luas alas (La) | La = π × r × r |
| Ltanpa tutup | Ltanpa tutup = La + Ls |
| Jari-jari (r) jika diketahui Volume | r = $\sqrt{\frac {V}{π \times t }}$ |
| Jari-jari (r) jika diketahui Luas Selimut | r = $\frac {Ls}{2 \times π \times t}$ |
| Jari-jari (r) jika diketahui Luas Permukaan | Faktor dari $r^{2} +rt - \frac {L}{2 \times π} = 0$ |
| Tinggi (t) jika diketahui Volume | $t = \frac {V}{π \times r^{2}}$ |
| Tinggi (t) jika diketahui Luas Selimut | $t = \frac {Ls}{2 \times π \times r}$ |
| Tinggi (t) jika diketahui Luas Permukaan | $t = \frac {L}{2 \times π \times r} - r$ |
Keterangan:
t = tinggi
jari-jari (r) = d÷2
diameter (d) = 2×r
π = 22/7 untuk jari-jari kelipatan 7 dan 3,14 untuk jari-jari bukan kelipatan 7
6. Kerucut
Kerucut merupakan sebuah bangun ruang yang mempunyai alas berbentuk lingkaran dan dengan selimut yang berbentuk irisan dari lingkaran. Untuk lebih lengkapnya baca di Rumus Kerucut.
| Nama | Rumus |
|---|---|
| Volume (V) | $V = \frac {1}{3} \times π \times r \times r \times t$ $V = \frac {1}{3} \times π \times r^2 \times t$ |
| Luas permukaan (L) | L = La + Ls = (π x r2) + (π x r x s) = π x r x (r + s) |
| Luas alas (La) | La = π x r x r = π x r2 |
| Luas selimut (Ls) | Ls = π x r x s |
| Jari-jari (r) diketahui V | r = $\sqrt{\frac {3 \times V}{π \times t}}$ |
| Jari-jari (r) diketahui L | Faktor dari $r^2 + rs - \frac {L}{π} = 0$ |
| Jari-jari (r) diketahui Ls | r = $\frac {Ls}{π \times s}$ |
| Tinggi (t) diketahui V | $t = \frac {3 \times V}{π \times r \times r}$ |
Keterangan:
t = tinggi
r = jari-jari
s = panjang garis pelukis (apotema), merupakan garis yang menghubungkan titik puncak dengan titik keliling alas kerucut.
Nilai s dapat dihitung menggunakan rumus Pythagoras.
s = $\sqrt{r^2 + t^2}$
π = 22/7 untuk jari-jari (r) kelipatan 7 dan 3,14 untuk jari-jari bukan kelipatan 7
7. Bola
Bola merupakan sebuah bangun ruang tiga dimensi di mana permukaannya memiliki jarak yang sama terhadap titik pusatnya. Bola merupakan bangun ruang yang dibatasi oleh sisi lengkung. untuk lebih lengkapnya silahkan baca di Rumus Bola.
| Nama | Rumus |
|---|---|
| Volume (V) | $V = \frac {4}{3} \times π \times r^3$ |
| Luas Permukaan (L) | $L = 4 \times π \times r^2$ |
| Jari-jari (r) diketahui V | $r = \sqrt[3]{\frac {3 \times V}{4 \times π}}$ |
| Jari-jari (r) diketahui L | $r = \sqrt{\frac {L}{4 \times π}}$ |
Keterangan:
Demikian pembahasan tentang bangun ruang dan rumus bangun ruang semoga bermanfaat dan menambah ilmu pengetahuan kita semua.()
jari-jari (r) = d÷2
diameter (d) = 2×r
π = 22/7 untuk jari-jari kelipatan 7 dan 3,14 untuk jari-jari bukan kelipatan 7