√ Prisma | Rumus Volume Prisma dan Luas Permukaan Prisma
Rumus Prisma - Materi Matematika Pengertian dan Rumus Prisma – Definisi, Luas Permukaan, Volume dan Contoh Soal Prisma Segitiga beserta pembahasannya lengkap.
Dalam geometri, prisma adalah bangun ruang tiga dimensi yang dibatasi oleh dua buah bidang sejajar yang sama besar dimana bidang-bidang tersebut adalah alas dan tutup.
Bidang sisi atap dan sisi alas prisma bersifat kongruen artinya kedua sisi tersebut memiliki ukuran dan bentuk yang sama.
Nama sebuah prisma ditentukan oleh bentuk alasnya dan kedudukan rusuk tegaknya.
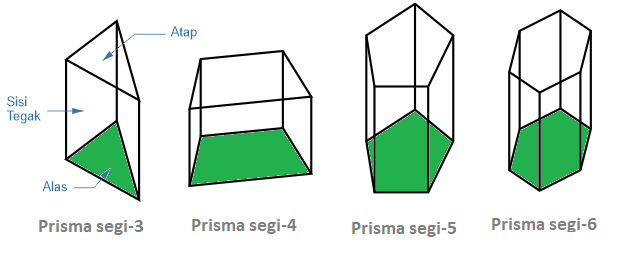
Jika sebuah prisma memiliki alas berbentuk segi n, maka prisma tersebut bernama prisma segi n. Misalnya segi-3 (prisma segitiga) dan segi-4 (prisma segi empat: prisma trapesium dan prisma jajar genjang).
1. Bentuk alas dan atap prisma bersifat kongruen (sama dan sebangun).
2. Alas dan atap prisma memiliki bentuk segi-n, misalnya segitiga.
3. Semua bidang sisi tegak prisma berbentuk segi empat atau persegi panjang.
4. Jumlah semua sisi prisma adalah n+2, contoh:
Prisma yang mempunyai alas sampai segi-n yang jika berupa titik-titik tak terhingga, yang umumnya disebut dengan tabung.
Jika sebuah bangun ruang diiris beberapa rusuknya kemudian direbahkan pada suatu bidang datar, hasil yang ada di bidang datar tersebut dinamakan jaring-jaring bangun ruang. Perhatikan gambar dibawah ini.
Keenam jaring-jaring tersebut merupakan jaring-jaring prisma segitiga, prisma segi empat, prisma segi lima, prisma segi enam, prisma segi tujuh, dan prisma segi delapan.
Kita bisa dengan mudah menemukan bentuk prisma dalam kehidupan sehari-hari, beberapa diantaranya adalah:
Keterangan :
n = segi dalam prisma/banyak sudut misal prisma segitiga, artinya n = 3
t = tinggi prisma
Luas Alas = sesuai dengan bentuk prisma
Rumus Luas alas prisma segitiga = 1/2 x alas x tinggi.
Daftar Isi
A. Pengertian Prisma
Bidang sisi atap dan sisi alas prisma bersifat kongruen artinya kedua sisi tersebut memiliki ukuran dan bentuk yang sama.
Nama sebuah prisma ditentukan oleh bentuk alasnya dan kedudukan rusuk tegaknya.
Jika sebuah prisma memiliki alas berbentuk segi n, maka prisma tersebut bernama prisma segi n. Misalnya segi-3 (prisma segitiga) dan segi-4 (prisma segi empat: prisma trapesium dan prisma jajar genjang).
B. Ciri-Ciri Prisma
1. Bentuk alas dan atap prisma bersifat kongruen (sama dan sebangun).
2. Alas dan atap prisma memiliki bentuk segi-n, misalnya segitiga.
3. Semua bidang sisi tegak prisma berbentuk segi empat atau persegi panjang.
4. Jumlah semua sisi prisma adalah n+2, contoh:
- Prisma segitiga = n+2 = 3+2 = 5 buah sisi
- Prisma segi empat = n+2 = 4+2 = 6 buah sisi
- Prisma segi lima = n+2 = 5+2 = 7 buah sisi
- Prisma segi enam = n+2 = 6+2 = 8 buah sisi
- Prisma segitiga = 3xn = 3x3 = 9 buah rusuk
- Prisma segi empat = 3xn = 3x4 = 12 buah rusuk
- Prisma segi lima = 3xn = 3x5 = 15 buah rusuk
- Prisma segi enam = 3xn = 3x6 = 18 buah rusuk
- Prisma segitiga = 2xn = 2×3 = 6 buah titik sudut
- Prisma segi empat = 2xn = 2×4 = 8 buah titik sudut
- Prisma segi lima = 2xn = 2×5 = 10 buah titik sudut
- Prisma segi enam = 2xn = 2×6 = 12 buah titik sudut
C. Macam-Macam Prisma
Prisma Segitiga
Prisma segitiga adalah sebuah bangun ruang tiga dimensi yang mempunyai alas dan atap yang berbentuk segitiga.Prisma Segiempat
Prisma segiempat mempunyai nama lain kubus jika semua sisi-sisinya sama panjang dan balok jika semua sisinya tidak sama panjang.Prisma Segilima
Prisma segilima adalah bangun ruang tiga dimensi yang mempunyai atap dan alas berbentuk segilima.Prisma Segienam
Merupakan bangun ruang tiga dimensi yang memiliki alas dan atap berbentuk segienam.Prisma yang mempunyai alas sampai segi-n yang jika berupa titik-titik tak terhingga, yang umumnya disebut dengan tabung.
D. Jaring-jaring Prisma
Jika sebuah bangun ruang diiris beberapa rusuknya kemudian direbahkan pada suatu bidang datar, hasil yang ada di bidang datar tersebut dinamakan jaring-jaring bangun ruang. Perhatikan gambar dibawah ini.
Keenam jaring-jaring tersebut merupakan jaring-jaring prisma segitiga, prisma segi empat, prisma segi lima, prisma segi enam, prisma segi tujuh, dan prisma segi delapan.
E. Contoh Benda Berbentuk Prisma dalam Kehidupan Sehari-hari
Kita bisa dengan mudah menemukan bentuk prisma dalam kehidupan sehari-hari, beberapa diantaranya adalah:
- tenda perkemahan
- kue ulang tahun yang telah dipotong
- atap rumah
- jepitan kertas
- alat pengumpul sampah
- penahan roda (ganjal)
F. Rumus Prisma
- Rumus luas permukaan prisma = (2 x Luas alas) + Keliling alas x tinggi
- Luas Permukaan Prisma Segi-3 L = (2 x Luas alas) + ( a1 + a2 + a3) x t
- Luas Permukaan Prisma Segi-4 L = (2 x Luas alas) + ( a1 + a2 + a3 + a4) x t
- Luas Permukaan Prisma Segi-5 L = (2 x Luas alas) + ( a1 + a2 + a3 + a4 + a5) x t
- Luas Permukaan Prisma Segi-6 L = (2 x Luas alas) + ( a1 + a2 + a3 + a4 + a5 + a6) x t
- tinggi (t) jika diketahui V, t = V ÷ Luas Alas
- Rumus volume prisma = luas alas x tinggi
- Rumus mencari banyak rusuk = 3 x n
- Rumus mencari banyak sisi = n + 2
- Rumus mencari banyak titik sudut = 2 x n
Keterangan :
n = segi dalam prisma/banyak sudut misal prisma segitiga, artinya n = 3
t = tinggi prisma
Luas Alas = sesuai dengan bentuk prisma
G. Luas Alas Prisma
Rumus Luas alas prisma segitiga = 1/2 x alas x tinggi.
Rumus Luas alas prisma segiempat
- Rumus Luas alas prisma segiempat dengan alas berbentuk balok = p x l x t
- Rumus Luas alas prisma segiempat dengan alas berbentuk kubus = sisi x sisi x sisi
H. Cara Menghitung Volume Prisma
Contoh Soal Menghitung Volume Prisma:
Sebuah prisma mempunyai alas berbentuk segitiga siku-siku dengan panjang sisi 16 cm, 20 cm dan tinggi prisma tersebut adalah 30 cm. Hitunglah volume prisma tersebut!
Pembahasan :
Diketahui :
sisi segitiga : 16 cm, 20 cm
tinggi prisma : 30 cm
Ditanya : Volume prisma ?
Jawab :
V = Luas alas × t
Karena alas prisma berbentuk segitiga, maka
a = 16 cm, sebagai alas (a) dan b = 20 cm sebagai tinggi (t)
La = ½ × a × t
La = ½ × 16 cm × 20 cm
La = 160 cm²
Sehingga Volume Prisma
V = Luas alas × t
V = 160 cm² × 30 cm
V = 4800 cm³
I. Cara Menghitung Luas Permukaan Prisma
Contoh Soal Menghitung Luas Permukaan Prisma:
Perhatikan gambar diatas
Dapat kita ketahui masing-masing rusuk pada alasnya
a1= 24 cm
a2 =20 cm
a3 = 16 cm
Dan t = 30 cm
Sehingga
Luas permukaan prisma = 2×(luas alas) + (keliling alas)×tinggi
Luas permukaan prisma = 2×(½×16×20) + {(16+20+24)×30}
Luas permukaan prisma = 2 x 160 + ( 60 x 30 )
Luas permukaan prisma = 320 + 1800
Luas permukaan prisma = 2120 cm²
J. Cara Menghitung Tinggi Prisma
Contoh Soal Menghitung Tinggi Prisma:
Perhatikan gambar diatas, jika volume prisma tersebut adalah 400 cm³. Berapakah tinggi prisma tersebut?
Pembahasan :
Diketahui :
V = 400 cm³
Alas prisma berbentuk segitiga
Ditanya:
Tinggi prisma (t)
Penyelesaian:
t = V ÷ Luas Alas
Sebelumnya harus dihitung luas alas prisma, dari gambar diatas bisa kita ketahui
Alas berbentuk segitiga dengan
alas segitiga = 10 cm
tinggi segitiga = 8 cm
Maka luas alas prisma bisa dihitung dengan rumus luas segitiga
LΔ = ½ × alas segitiga × tinggi segitiga
LΔ = ½ × 10 cm × 8 cm
LΔ = 40 cm²
L alas = 40 cm²
Maka tinggi prisma tersebut
t = V ÷ Luas Alas
t = 400 cm³ ÷ 40 cm²
t = 10 cm
Jadi, tinggi prisma adalah 10 cm.
Sekian artikel “Prisma | Rumus Volume Prisma dan Luas Permukaan Prisma”. Terima kasih dan semoga bermanfaat…
Baca juga tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel “Prisma | Rumus Volume Prisma dan Luas Permukaan Prisma”. Terima kasih dan semoga bermanfaat…