Rumus Volume Kerucut dan Luas Permukaan Kerucut

Oleh Admin

Rumus Volume Kerucut dan Luas Permukaan Kerucut - Setelah sebelumnya kita membahas tentang salah satu bangun ruang yaitu tabung sekarang kita akan mencoba membahas bangun ruang berikutnya yaitu kerucut.

Pengertian Kerucut

Kerucut mempunyai pengertian sebuah bangun ruang yang mempunyai alas berbentuk lingkaran dan dengan selimut yang berbentuk irisan dari lingkaran.

Kerucut merupakan salah satu bangun ruang sejenis limas yang istimewa.

Ciri Ciri Kerucut

Berikut ini adalah ciri-ciri, sifat-sifat bangun ruang kerucut.

Memiliki dua buah bidang sisi yaitu satu buah bidang sisi lingkaran yang merupakan alasnya dan satu bidang selimut
Memiliki 1 buah rusuk
Mempunyai 1 titik puncak

Unsur Unsur Kerucut

Sama seperti bangun ruang yang lain kerucut juga mempunyai unsur-unsur yang menyusunnya, berikut ini adalah unsur-unsur bangun ruang kerucut.

Alas, yaitu sisi yang berbentuk lingkaran.(daerah berwarna ungu)
Diameter alas (d), yaitu garis AB.
Jari-jari alas (r), yaitu garis AD dan garis BD.
Tinggi kerucut (t), yaitu jarak dari titik puncak kerucut ke pusat bidang alas (garis CD).
Selimut kerucut, yaitu sisi kerucut berupa sisi tegak/lengkung.
Garis pelukis (s), yaitu garis-garis pada selimut kerucut yang ditarik dari titik puncak C ke titik pada alas lingkaran.

Jari-Jari Kerucut

Jari-jari kerucut adalah panjang garis yang menghubungkan titik pusat lingkaran dengan titik yang ada pada lingkaran alas kerucut.

Diameter alas kerucut adalah panjang garis yang menghubungkan dua buah titik pada lingkaran alas yang melalui titik pusat lingkaran alas kerucut.

Panjang sebuah diameter lingkaran sama dengan dua kali panjang sebuah jari-jari lingkaran.

Tinggi Kerucut

Tinggi kerucut adalah jarak antara titik pusat alas terhadap titik puncak kerucut.

Jika kita membuat sebuah garis yang menghubungkan titik pusat alas dengan titik puncak kerucut maka didapat sebuah ruas garis tegak lurus dengan bidang alas. Panjang garis ini adalah tinggi kerucut.

Selimut Kerucut

Selimut kerucut adalah sebuah sisi lengkung yang membungkus kerucut. Terletak di antara alas dan titik puncak kerucut. Selimut kerucut berbentuk juring lingkaran.

Garis Pelukis Kerucut

Garis pelukis (apotema ) adalah ruas garis/sisi miring yang menghubungkan titik puncak dengan titik keliling pada alas kerucut.

Garis pelukis, tinggi kerucut, dan jari-jari kerucut membentuk sebuah segitiga siku-siku, sehingga berlaku rumus phytagoras untuk menghitung hubungan ketiga unsur tersebut.

Rusuk Kerucut

Secara sederhana, pengertian rusuk adalah sebuah garis dalam bangun ruang yang menjadi titik potong dua sisi atau garis bertemunya dua sisi.

Kerucut sendiri mempunyai 2 sisi, yaitu sisi datar yang merupakan alasnya dan sisi lengkung yang merupakan selimutnya.

Kedua sisi tersebut bertemu pada satu garis lengkung di bawah sisi lengkung yang berimpit dengan keliling sisi alasnya sehingga rusuk kerucut juga berbentuk garis lengkung yang membentuk lingkaran.

Agar lebih jelas perhatikan gambar di atas, Terlihat pada gambar, rusuk kerucut mengikuti keliling sisi alasnya.

Jadi, dari penjelasan di atas bisa kita simpulkan, benar jika KERUCUT MEMPUNYAI RUSUK.

Titik Sudut Kerucut

Titik sudut adalah titik pertemuan antara 3 rusuk atau 3 sisi dalam sebuah bangun ruang.

Sebuah limas segi empat beraturan jika alasnya secara bertahap diubah menjadi segi-n beraturan dan diteruskan hingga n menjadi sangat besar, maka limas itu “akan berubah” menjadi kerucut.

Jadi titik sudut pada puncak limas tersebut berubah menjadi titik sudut puncak kerucut(pemahaman ini hanya untuk guru).

Kesimpulannya kerucut tidak memiliki titik sudut, hanya saja disebut dengan titik puncak dan agar mudah dipahami (SD) dikatakan kerucut tidak memiliki titik sudut.

Rumus Kerucut

Keterangan:
π = Phi, 22/7 untuk jari-jari (r) kelipatan 7 dan 3,14 untuk jari-jari bukan kelipatan 7
r = Jari-jari
t = Tinggi kerucut tersebut
s = Garis pelukis

Panjang s bisa dihitung memakai rumus Pythagoras.

s = $\sqrt{r^2+t^2}$

Nama	Rumus
Volume (V)	$V = \frac {1}{3} \times π \times r^2 \times t$ $V = \frac {1}{3} \times π \times r \times r \times t$
Luas permukaan (L)	$L = La + Ls$ $\,\,\,\,\,= (π \times r^2)+(π \times r \times s)$ $\,\,\,\,\,= π \times r \times (r + s)$
Luas alas (La)	$La = π \times r \times r$ $\,\,\,\,\,\,\,= π \times r^2$
Luas selimut (Ls)	$Ls = π \times r \times s$
Jari-jari (r) diketahui V	$r = \sqrt{\frac {3 \times V}{π \times t}}$
Jari-jari (r) diketahui L	$Faktor\,dari$ $r^2 + rs - \frac {L}{π} = 0$
Jari-jari (r) diketahui Ls	$r = \frac {Ls}{π \times s}$
Tinggi (t) diketahui V	$t = \frac {3 \times V}{π \times r \times r}$

Volume Kerucut

Volume kerucut atau isi kerucut adalah ruang yang terdapat di dalam bangun kerucut. Misalkan sebuah kerucut yang terbuat dari plastik yang di isi air mempunyai volume satu centimeter kubik maka jumlah volume air yang bisa mengisi ruang di dalam kerucut tersebut adalah 1 centimeter kubik.

$V = \frac {1}{3} \times π \times r^2 \times t$
atau
$V = \frac {1}{3} \times π \times r \times r \times t$

Keterangan:
r = jari-jari
t= tinggi
π= phi(22/7 atau 3,14)

Luas Alas Kerucut

Karena berbentuk lingkaran sehingga luas alas kerucut dapat dihitung memakai rumus:

La = π x r²( lihat rumus lingkaran disini )

Luas Selimut Kerucut

Selimut kerucut jika dibentangkan bentuknya adalah berupa juring lingkaran dengan panjang busur sama dengan keliling lingkaran alas.

Sehingga luas selimut kerucut yang mempunyai bentuk irisan lingkaran luas nya bisa dihitung memakan rumus:

Ls = π x r x s

Luas Permukaan Kerucut

Luas permukaan kerucut merupakan jumlah luas alas di tambah luas selimutnya. sehingga rumusnya adalah:

L = La + Ls
L = ( π x r² ) + ( π x r x s )
L = π x r x ( s + r )

Jadi rumus luas permukaan kerucut adalah L = π x r x ( s + r )

Contoh Soal Kerucut

Contoh Soal Volume Kerucut

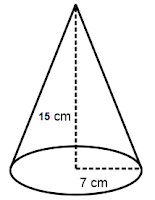
Sebuah bangun kerucut memiliki tinggi 15 cm dan jari-jari 7 cm. Hitunglah berapa volume kerucut tersebut!

Penyelesaian:

Diketahui:

jari-jari (r) = 7 cm

Tinggi (t ) = 15 cm

Ditanya:

Volume kerucut (V) =...?

Jawab:

$V = \frac {1}{3} \times π \times r \times r \times t$

$V = \frac {1}{3} \times \frac {22}{7} \times 7 \times 7 \times 15$

$V = \frac {1}{3} \times \frac {22}{7} \times 49 \times 15$

$V = \frac {1}{3} \times \frac {22}{7} \times 735$

$V = \frac {1}{3} \times 2310$

$V = \frac {2310}{3}$

$V = 770$

Jadi volume kerucut tersebut adalah 770 cm³

Contoh Soal Luas Permukaan Kerucut

Sebuah bangun kerucut memiliki tinggi 24 cm dan jari-jari 7 cm. Hitunglah berapa luas permukaan kerucut tersebut!

Penyelesaian:

Diketahui:

jari-jari (r) = 7 cm

Tinggi (t ) = 24 cm

Ditanya:

Luas permukaan (L) =...?

Jawab:

Pertama kita cari panjang garis pelukis (s)

Panjang garis pelukis dapat dihitung dengan rumus Pythagoras

s = $\sqrt{r^2+t^2}$

s = $\sqrt{7^2+24^2}$

s = $\sqrt{49+576}$

s = $\sqrt{625}$

s = 25 cm

Kemudian kita hitung luas permukaannya

L = π x r x ( s + r )

L = $\frac {22}{7}$ x 7 x ( 25 + 7 )

L = $\frac {22}{7}$ x 7 x ( 32 )

L = $\frac {22}{7}$ x 224

L = $\frac {4928}{7}$

L = 704 cm

Jadi luas permukaan kerucut tersebut adalah 704 cm²

Contoh Soal Mencari Jari-Jari Kerucut Jika Diketahui Volume dan Tingginya

Sebuah bangun kerucut memiliki tinggi 14 cm dengan volume 308 cm³, Hitunglah jari-jari kerucut tersebut!

Diketahui:

t = 14 cm

V = 308 cm³

Ditanya:

Jari-jari kerucut (r) = ...?

Jawab:

Cara menghitung jari-jari kerucut diketahui volume

$r = \sqrt{\frac {3 \times V}{π \times t}}$

$r = \sqrt{\frac {3 \times 308}{\frac {22}{7} \times 14}}$

$r = \sqrt{\frac {924}{44}}$

$r = 21$

Jadi, jari-jari kerucut tersebut adalah 21 cm.

Contoh Soal Mencari Jari-Jari Kerucut Jika Diketahui Luas Selimut dan Garis Pelukis

Sebuah bangun kerucut memiliki panjang garis pelukis 15 cm dan luas selimut 423,9 cm², Hitunglah jari-jari kerucut tersebut!

Diketahui:

Ls = 423,9 cm²

s = 15

Ditanya:

Jari-jari kerucut (r) = ...?

Jawab:

Rumus Jari-jari (r) diketahui Ls adalah:

$r = \frac {Ls}{π \times s}$

Karena jari-jari bukan kelipatan 7 maka nilai π adalah 3,14

$r = \frac {Ls}{π \times s}$

$r = \frac {423,9}{3,14 \times 15}$

$r = \frac {423,9}{47,1}$

$r = 9$

Jadi, jari-jari kerucut tersebut adalah 9 cm.

Contoh Soal Mencari Tinggi Kerucut Jika Diketahui Volume

Hitunglah tinggi kerucut yang mempunyai jari-jari 5 cm dengan volume 314 cm³ ...

Diketahui:

r = 5 cm

V = 314 cm³

Ditanya:

Tinggi kerucut (t) = ...?

Jawab:

Karena jari-jari bukan kelipatan 7, maka nilai π = 3,14

Cara menghitung tinggi kerucut diketahui volume

$t = \frac {3 \times V}{π \times r \times r}$

$t = \frac {3 \times 314}{3,14 \times 5 \times 5}$

$t = \frac {942}{78,5}$

$t = 12$

Jadi, tinggi kerucut tersebut adalah 12 cm.

Contoh Benda yang Berbentuk Kerucut

Caping(untuk penutup kepala petani)
Topi ulang tahun(sebagai hiasan kepala)
Corong air(untuk memindahkan air)
Terompet(alat musik)
Gelas kerucut(sebagai gelas hias)
Kap lampu
Tutup saji
Kukusan
Cone ice cream

Setelah melihat pembahasan rumus di atas bagaimana pendapat kamu, Mudah bukan ? Semoga pembahasan tentang rumus volume kerucut dan rumus luas permukaan kerucut bermanfaat bagi pembaca semua.()

Referensi

R. Soedjadi, (2000). Kiat Pendidikan Matematika di Indonesia, Konstatasi keadaan masa kini menuju harapan masa depan. Direktorat Jendral Pendidikan Tinggi Departemen Pendidikan Nasional.
Gambar gif Kerucut: Pierce, Rod - Math is Fun