Pengertian Bilangan Bulat, Operasi dan Contohnya
Pengertian Bilangan Bulat dan Contohnya - Pada kesempatan kali ini kita akan membahas mengenai bilangan bulat lengkap beserta contohnya.
Sebelum kita membahas lebih detail mengenai apa itu pengertian bilangan bulat ada baiknya terlebih dahulu kita mengetahui apa itu maksud dan pengertian bilangan.
Pengertian bilangan
Pengertian bilangan adalah suatu konsep dalam matematika yang dipakai sebagai pencacahan serta pengukuran.Nah agar lebih jelas lagi kamu bisa membaca tulisan sebelumnya mengenai pengertian bilangan, Baca disini Pengertian Bilangan dan Macam-Macam Bilangan.
Selain itu juga bilangan bulat tidak memiliki bilangan terkecil ataupun bilangan terbesar.
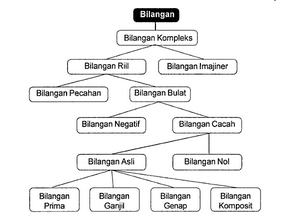
Nah agar lebih jelas lagi untuk memahami pengertian bilangan bulat kamu bisa melihat gambar struktur bilangan di bawah ini.
Daftar Isi
A. Pengertian Bilangan Bulat
Bilangan Bulat adalah bilangan yang terdiri dari bilangan bulat positif, bilangan nol serta bilangan bulat negatif.
Bilangan bulat yang dilambangkan dengan huruf ℤ adalah anggota bilangan rasional yang terdiri dari bilangan bulat negatif, nol, dan bilangan bulat positif.
Dari definisi di atas, didapati bahwa bilangan bulat terdiri dari tiga jenis bilangan yaitu bilangan bulat negatif, bilangan bulat nol, dan bilangan bulat positif.
Bilangan-bilangan tersebut selanjutnya dituliskan seperti berikut ini.
Bentuk di atas juga dapat dinyatakan dalam sebuah garis bilangan seperti gambar di bawah ini.
Dari pengertian di atas bisa kita ambil kesimpulan jika bilangan bulat adalah himpunan bilangan yang termasuk didalamnya adalah bilangan cacah, bilangan asli, bilangan prima, bilangan komposit, bilangan nol, bilangan satu, bilangan negatif, bilangan ganjil dan bilangan genap.
Z = { …, -4 , -3, -2, -1, 0 , 1, 2, 3, 4, … }
Bentuk di atas juga dapat dinyatakan dalam sebuah garis bilangan seperti gambar di bawah ini.
Dari pengertian di atas bisa kita ambil kesimpulan jika bilangan bulat adalah himpunan bilangan yang termasuk didalamnya adalah bilangan cacah, bilangan asli, bilangan prima, bilangan komposit, bilangan nol, bilangan satu, bilangan negatif, bilangan ganjil dan bilangan genap.
Selain itu juga bilangan bulat tidak memiliki bilangan terkecil ataupun bilangan terbesar.
Nah agar lebih jelas lagi untuk memahami pengertian bilangan bulat kamu bisa melihat gambar struktur bilangan di bawah ini.
B. Jenis Jenis Bilangan Bulat
Secara sederhana bilangan bulat terdiri dari:- Bilangan bulat positif.
- Bilangan nol.
- Bilangan bulat negatif.
Pengertian Bilangan Bulat Positif
Bilangan bulat positif adalah bilangan yang dimulai dari bilangan satu ke atas dan seterusnya. Contoh bilangan bulat positif : { 1, 2, 3, 4, 5,dan seterusnya }.Pengertian Bilangan Bulat Negatif
Bilangan bulat negatif adalah bilangan yang dimulai dari bilangan negatif satu ke bawah dan seterusnya. Contoh bilangan bulat negatif : { dan seterusnya -5, -4, -3, -2, -1 }.Bilangan Nol
Bilangan nol (0) Nol bukan bilangan positif atau pun bilangan negatif.
C. Garis Bilangan Bulat
Garis bilangan digunakan untuk memudahkan melakukan perhitungan bilangan bulat, penjumlahan dan pengurangan bilangan bisa dilakukan dengan bantuan garis bilangan bulat.
D. Contoh Soal Bilangan Bulat
Untuk mempermudah dalam memahami penjelasan di atas, maka pahamilah contoh soal di bawah ini.
Contoh:
Tentukan himpunan bilangan bulat di antara -6 sampai dengan 5 !
Jawab:
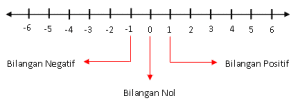
Untuk mempermudah dalam menentukan bilangan bulat di antara -6 sampai dengan 5, kita dapat menggambarkan bilangan-bilangan tersebut pada garis bilangan seperti gambar di bawah ini.
Dari gambar di atas, didapati bahwa bilangan-bilangan bulat yang terletak di antara -6 dan 5 adalah -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5 atau bisa dinyatakan dalam bentuk himpunan yaitu {-6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5}.
E. Operasi Hitung Bilangan Bulat
Pada sub pembahasan pengertian bilangan bulat disebutkan bahwa bilangan bulat merupakan bagian dari bilangan rasional.Dengan demikian, operasi hitung yang berlaku pada bilangan bulat sama seperti operasi hitung pada bilangan rasional.
Contoh:
E1. Penjumlahan Bilangan Bulat
Untuk memahami operasi penjumlahan bilangan bulat, perhatikanlah contoh di bawah ini.Contoh:
Dengan menggunakan garis bilangan, tentukan hasil penjumlahan -4 +6!
Jawab:
Pada gambar garis bilangan di atas, -4 menunjukkan pergeseran dari titik 0 menuju ke kiri kea rah titik -4. Karena ditambah 6, pergeseran berubah arah menuju kanan sebanyak 6 langkah.
Dengan demikian, didapati titik akhir yaitu 3. Dari hal tersebut, maka diperoleh bahwa -4 + 6 =2.
Berdasarkan penjelasan di atas, maka penjumlahan dua bilangan bulat dapat dinyatakan dalam bentuk berikut ini.
Berdasarkan penjelasan di atas, maka penjumlahan dua bilangan bulat dapat dinyatakan dalam bentuk berikut ini.
a + b = c
dimana a, b, dan c adalah bilangan bulat
|
Sifat sifat Penjumlahan Bilangan Bulat
Operasi hitung yang dilakukan antar bilangan bulat tentunya memunculkan sifat-sifat tertentu.
Berikut beberapa sifat operasi hitung penjumlahan bilangan bulat dimana a, b dan c adalah sembarang bilangan bulat.
1. a + b = b + a (sifat komutatif)
1. a + b = b + a (sifat komutatif)
Contoh: 10 + (-3) = -3 +10 = 7
2. (a + b) + c = a + (b + c) (sifat asosiatif)
Contoh: (-1 + 2) + 3 = -1 + (2 + 3) = 4
3. a + 0 = 0 + a = a (sifat identitas)
Contoh: -2 + 0 = 0 + (-2) = -2
4. a + b = c, maka c juga bilangan bulat (sifat tertutup)
Contoh: 6 + (-4) = 2 (6,-4, dan 3 adalah bilangan bulat semua).
Untuk mempermudah dalam memahami bentuk di atas, cermatilah beberapa contoh di bawah ini.
Contoh:
E2. Pengurangan Bilangan Bulat
Pengurangan merupakan kebalikan dari operasi hitung penjumlahan. Misalkan dipunyai bilangan bulat a, b, dan c, maka operasi pengurangan bilangan bulat dapat dituliskan sebagai berikut.
a - b = a + (-b) = c
dimana a, b, dan c adalah bilangan bulat
|
Untuk mempermudah dalam memahami bentuk di atas, cermatilah beberapa contoh di bawah ini.
Contoh:
a. -7 - 8 = -7 + (-8) =- 15
b. -6 - (-12) = -6 + 12 = 6
c. 6 - (-15) = 6 + 15 = 21
E3. Perkalian Bilangan Bulat
Misalkan dipunyai sembarang bilangan bulat a dan b. Perkalian a x b adalah penjumlahan berulang dari b sebanyak a kali. Misalnya:1 × (-5) = -5
2 × (-5) = (-5) + (-5) = -10
3 × (-5) = (-5) + (-5) + (-5) = -15
Pada perkalian bilangan bulat a,b, di atas, maka berlaku:
a × b = ab
a × (-b ) = -ab
(-a) × b = -ab
(-a) × (-b) = ab
Operasi tanda bilangan bulat:
negatif x positif = negatif
positif x negatif = negatif
negatif x negatif = positif
positif x positif = positif
Untuk lebih mempermudah dalam memahami operasi perkalian di atas, perhatikan contoh-contoh berikut ini.
Contoh:
11 × 4 = 44
4 × (-6) = -24
(-8) × 6 = -48
(-8) × (-4) = 32
Sifat sifat Perkalian Bilangan Bulat
Karena bilangan bulat adalah bagian dari bilangan rasional, maka sifat-sifat operasi hitung perkalian yang berlaku pada bilangan rasional juga berlaku pada bilangan bulat.
Untuk sembarang bilangan bulat a, b, dan c, maka berlaku sifat-sifat berikut ini:
a × b = b × a (sifat komutatif)
a × b = b × a (sifat komutatif)
Contoh: 6 × (-2) = -2 × 6 = -12
(a × b) × c = a × (b × c) (sifat asosiatif)
Contoh: (-1 × 2) × 3 = -1 × (2 × 3) = -6
a × 0 = 0 × a = 0 (sifat identitas)
Contoh: 8 × 0 = 0 × 8 = 0
a × 1/a = 1 (sifat invers)
Contoh: 6 × 1/6 = 1
c × (a + b) = (c × a) + (c × b) (sifat distributif)
Contoh: 2 × (4 + 7) = (2 × 4) + (2 × 7) = 8 + 14 = 22
a × b = c, maka c juga bilangan bulat.........(sifat tertutup)
Contoh: 6 × (-1) = -6. (6 dan -1 adalah bilangan bulat, -6 juga bilangan bulat)
operasi kebalikan disebut juga dengan invers perkalian. Untuk lebih jelasnya, perhatikan contoh-contoh berikut ini.
Contoh:
E4. Pembagian Bilangan Bulat
Pembagian adalah operasi kebalikan dari perkalian yang dapat dituliskan sebagai berikut.operasi kebalikan disebut juga dengan invers perkalian. Untuk lebih jelasnya, perhatikan contoh-contoh berikut ini.
Contoh:
48 : 12 = 48 x 1/12 = 4
-64 : 4 = -64 x 1/4 = -16
Dalam operasi hitung pembagian bilangan bulat, kita mengenal dua jenis pembagian yaitu pembagian antar bilangan bulat dengan bilangan bulat bukan nol dan pembagian bilangan bulat dengan bilangan nol.
-64 : 4 = -64 x 1/4 = -16
Dalam operasi hitung pembagian bilangan bulat, kita mengenal dua jenis pembagian yaitu pembagian antar bilangan bulat dengan bilangan bulat bukan nol dan pembagian bilangan bulat dengan bilangan nol.
Berikut ini akan dijelaskan mengenai kedua jenis pembagian tersebut.
Contoh:
Pembagian Bilangan Bulat dengan Bilangan Bulat bukan Nol
Misalkan dipunyai dua bilangan bulat, maka operasi pembagian antara dua bilangan bulat tersebut adalah sebagai berikut.- Bilangan bulat negatif dibagi dengan bilangan bulat positif menghasilkan bilangan bulat negatif.
- Bilangan bulat positif dibagi dengan bilangan bulat negatif sama dengan bilangan bulat negatif.
- Bilangan bulat negatif dibagi bilangan bulat negatif menghasilkan bilangan bulat positif.
Contoh:
-28 ∶ 2 = -14
64 ∶ (-8) = -8
-16 ∶ -16 = 1
Pembagian Bilangan Bulat dengan Nol
Misalkan 9 ∶ 0 = x ⟺ x × 0 = 9. Jelas tidak ada satu bilangan pun yang dapat digunakan sebagai pengganti x dalam perkalian bilangan bulat yang memenuhi x × 0 = 9 sehingga dapat disimpulkan sebagai berikut.Untuk setiap bilangan bulat a, maka hasil dari a : 0 adalah tidak terdefinisi
Uraian di atas dapat dipahami melalui beberapa contoh soal tentang pembagian bilangan bulat dengan nol berikut ini.
Contoh:
12 ∶ 0 = tidak terdefinisi
(-3) ∶ 0 = tidak terdefinisi
Pembagian Bilangan Bulat oleh Nol
Misalkan 0 ∶ a = b ⟺ b × a = 0. Adapun penyelesaian yang dapat digunakan sebagai pengganti b adalah 0 karena untuk perkalian 0 × a selalu menghasilkan 0. Maka, berdasarkan hal itu dapat ditarik kesimpulan berikut ini.Untuk sembarang bilangan bulat a dengan a ≠ 0 maka a ∶ 0 = 0.
Uraian di atas dapat dipahami melalui beberapa contoh soal tentang pembagian berikut ini.
Contoh:
0 ∶ 10 = 0
0 ∶ (-4) = 0
Nah demikian pembahasan mengenai Pengertian Bilangan Bulat dan Contohnya semoga bermanfaat bagi pembaca semua, jangan lupa like dan share jika bermanfaat ya.