✅Pengertian Bilangan Imajiner dan Contohnya
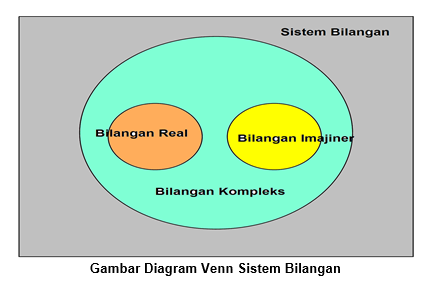
Dalam sistem bilangan, kita mengenal jenis bilangan kompleks. Bilangan kompleks adalah bilangan yang dapat dinyatakan dalam bentuk a +ib atau a + bi dengan a,b adalah sembarang bilangan real dan i adalah bilangan imajiner.
Daftar Isi
Bilangan ini dapat terbagi menjadi dua jenis kembali yaitu bilangan real dan bilangan imajiner.
Pada pembahasan kali ini, kita akan mempelajari tentang apa itu bilangan imajiner; sifat-sifat apa saja yang dimiliki oleh bilangan imajiner; dan operasi aljabar dari bilangan imajiner itu.
A. Pengertian Bilangan Imajiner
Pernahkah kalian menyelesaikan sebuah persamaan kuadrat dan mendapati akar persamaan tersebut adalah akar negatif? Jika iya, apa yang kalian lakukan?Apakah kalian menganggap bahwa persamaan kuadrat tersebut salah atau tidak memiliki akar? Untuk menjawab pertanyaan tersebut, perhatikan contoh bilangan berikut ini.
• √-1
• √-2
• √-4
• √-9
Bilangan-bilangan di atas adalah contoh bilangan imajiner karena memuat akar negatif.
Selain hal itu, alasan lain mengapa bilangan-bilangan itu dikatakan sebagai bilangan imajiner adalah karena bilangan-bilangan itu mempunyai sifat i² = -1 ⟺ i = √-1.
Berdasarkan uraian tersebut, maka bilangan imajiner dapat didefinisikan sebagai berikut.
Bilangan Imajiner atau yang dikenal dengan bilangan khayal adalah bilangan yang memiliki sifat i² = -1. Dengan kata lain, bilangan tersebut memiliki akar negatif.
Bilangan imajiner secara umum ditulis dalam bentuk bi, dengan b merupakan anggota bilangan real(b∈R) dan i adalah unsur imajiner.
B. Contoh Bilangan Imajiner
Berikut contoh bilangan imajiner.
• √-1
• √-2
• √-4
• √-9
• √-16
• √-20
Bilangan-bilangan di atas adalah contoh bilangan imajiner karena memuat akar negatif.
C. Mengubah Bilangan Imajiner menjadi Bilangan Kompleks
Bilangan imajiner merupakan bagian dari bilangan kompleks. Seperti diketahui, bilangan kompleks terdiri dari bilangan real dan bilangan imajiner.Dari hal tersebut, maka bilangan-bilangan imajiner dapat dikonversi menjadi bilangan kompleks.
Adapun langkah-langkah yang dilakukan untuk mengkonversi bilangan imajiner menjadi bilangan kompleks adalah sebagai berikut.
- Pilihlah bilangan imajiner √-a yang akan diubah menjadi bilangan kompleks.
- Selanjutnya, ubahlah bilangan imajiner √-a menjadi bentuk perkalian √a x √-1.
- Karena i = √-1 , maka ubah bentuk √a x √-1 menjadi √a x i ;
- Bentuk √a x i adalah bilangan kompleks yang didapat dari bilangan imajiner √-a
Untuk lebih memahami langkah-langkah di atas, pahamilah contoh-contoh soal di bawah ini.
Contoh Soal 1:
Ubahlah bilangan imajiner √-9 ke dalam bentuk bilangan kompleks!
Diberikan bilangan imajiner √-9, angka tersebut dapat diubah menjadi bentuk bi
√−9 = √9×(−1)
√−9 = √9×√−1
√−9 = 3×i
√−9 = 3i
Bentuk 3i adalah bilangan kompleks yang didapat dari bilangan imajiner √−9 .
Contoh Soal 2:
Ubahlah bilangan imajiner √-5 ke dalam bentuk bilangan kompleks!
Jawab:
bilangan imajiner √-5 diubah menjadi bilangan kompleks melalui perhitungan berikut:
√-5 = √5 x √-1
√-5 = √5 x i
Contoh Soal 3:
Ubahlah bilangan imajiner √-16 ke dalam bentuk bilangan kompleks!
Jawab:
bilangan imajiner √-16 diubah menjadi bilangan kompleks melalui perhitungan berikut:
√-16 = √16 x √-1
√-16 = 4 x i
√-16 = 4i
Contoh Soal 4:
Ubahlah bilangan imajiner √-20 ke dalam bentuk bilangan kompleks!
Jawab:
bilangan imajiner √-20 diubah menjadi bilangan kompleks melalui perhitungan berikut:
√-20 = √20 x √-1
√-20 = √4x5 x i
√-20 = 2√5 x i
Bentuk 2√5 x i adalah bilangan kompleks yang didapat dari bilangan imajiner √-20 .
D. Operasi Aljabar Bilangan Imajiner
Pada sub pembahasan sebelumnya sudah disebutkan bahwa bilangan imajiner merupakan bagian dari bilangan kompleks.Dengan demikian, semua operasi aljabar yang berlaku pada bilangan kompleks juga berlaku pada bilangan imajiner.
Berikut akan dijelaskan operasi-operasi aljabar jumlah dan kurang yang berlaku pada bilangan imajiner.
Operasi Penjumlahan
Misalkan dipunyai bilangan imajiner √-a dan √-b . Untuk mempermudah melakukan operasi penjumlahan pada bilangan imajiner, maka kita ubah terlebih dahulu kedua bilangan tersebut menjadi bilangan kompleks √a x i dan √b x i .Setelah itu, barulah dilakukan operasi penjumlahan pada kedua bilangan tersebut. Untuk lebih jelasnya, Perhatikan contoh-contoh berikut ini.
Contoh Soal:
Tentukan hasil penjumlahan antara √-20 dan √-45 !
Jawab:
Untuk √-20 , maka:
√-20 = √20 x √-1
√-20 = √4x5 x i
√-20 = 2√5 x i
√-45 = √45 x √-1
√-45 = √(9 x 5) x i
√-45 = 3√5 x i
√-20 + √-45 = (2√5 x i) + (3√5 x i)
√-20 + √-45 = (2√5 + 3√5) x i
√-20 + √-45 = 5√5 x i
√-20 + √-45 = 5√5 i
Jadi hasil √-20 + √-45 adalah 5√5 i
Operasi Pengurangan
Pada operasi pengurangan, cara yang digunakan sama seperti operasi penjumlahan yaitu: misalkan dipunyai bilangan imajiner √-a dan √-b.Kedua bilangan tersebut selanjutnya diubah dalam bentuk bilangan kompleks √a x i dan √b x i .
Selanjunya, barulah dilakukan operasi pengurangan pada kedua bilangan tersebut. Untuk lebih jelasnya, Perhatikan contoh berikut.
Contoh Soal:
Tentukan hasil dari √-45 - √-20 !
Jawab:
Untuk √-45 , maka:
√-45 = √45 x √-1
√-45 = √(9 x 5) x i
√-45 = 3√5 x i
Untuk √-20 , maka:
√-20 = √20 x √-1
√-20 = √4x5 x i
√-20 = 2√5 x i
√-45 - √-20 = (3√5 x i) - (2√5 x i)
√-45 - √-20 = (3√5 - 2√5) x i
√-45 - √-20 = √5 x i
√-45 - √-20 = √5 i
Jadi hasil √-45 - √-20 adalah √5 i
Materi lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel “Pengertian Bilangan Imajiner dan Contohnya“. Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share. Terima kasih…