√ KPK dan FPB (Pengertian, Cara Mencari dan Contoh Soal)
⭐⭐⭐Rangkuman kpk dan fpb, pengertian dan cara mencari kpk dan fpb termudah dilengkapi contoh soal dan penjelasannya..⭐⭐⭐
KPK dan FPB adalah salah satu materi yang diajarkan sejak bangku Sekolah Dasar (SD), kira-kira kamu masih ingat pelajarannya?
Khusus untuk kamu yang masih ada ingat walaupun sedikit tentang pelajaran ini pada artikel ini akan dijabarkan kembali mengenai KPK dan FPB, baik itu dari definisi, cara mencari, serta berbagai contoh soal mengenai KPK dan FPB.
Dalam mencari KPK dan FPB diperlukan hal tentang bilangan prima dan juga faktorisasi prima, apa sih maksud dari kedua kata tersebut.
Bilangan Prima adalah bilangan yang mungkin tidak asing lagi di telinga kamu yaitu bilangan asli yang hanya memiliki dua faktor yaitu bilangan itu sendiri dan 1, yang termasuk bilangan prima adalah {2, 3, 5, 7, 11, . . .}
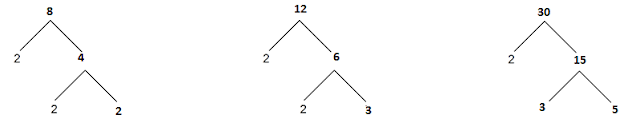
Faktorisasi prima adalah penguraian bilangan menjadi perkalian faktor-faktor prima. Nah, untuk melakukan faktorisasi prima ini kamu memerlukan pohon faktor
KPK = 2 X 2 X 2 X 2 X 5
KPK = 2 X 3 X 5 X 5
Daftar Isi
KPK dan FPB adalah salah satu materi yang diajarkan sejak bangku Sekolah Dasar (SD), kira-kira kamu masih ingat pelajarannya?
Khusus untuk kamu yang masih ada ingat walaupun sedikit tentang pelajaran ini pada artikel ini akan dijabarkan kembali mengenai KPK dan FPB, baik itu dari definisi, cara mencari, serta berbagai contoh soal mengenai KPK dan FPB.
Dalam mencari KPK dan FPB diperlukan hal tentang bilangan prima dan juga faktorisasi prima, apa sih maksud dari kedua kata tersebut.
Bilangan Prima adalah bilangan yang mungkin tidak asing lagi di telinga kamu yaitu bilangan asli yang hanya memiliki dua faktor yaitu bilangan itu sendiri dan 1, yang termasuk bilangan prima adalah {2, 3, 5, 7, 11, . . .}
Faktorisasi prima adalah penguraian bilangan menjadi perkalian faktor-faktor prima. Nah, untuk melakukan faktorisasi prima ini kamu memerlukan pohon faktor
Cara Mudah Mencari KPK dan FPB
Cara Mencari KPK (Kelipatan Persekutuan Terkecil)
Kelipatan Persekutuan Terkecil atau yang biasa dikenal di dunia pendidikan ialah KPK dari dua bilangan yang merupakan bilangan bulat positif terkecil yang dapat dibagi oleh kedua bilangan tersebut.
Dalam mencari nilai KPK dari bilangan kamu dapat menggunakan beberapa metode diantaranya kelipatan persekutuan, faktorisasi prima, dan menggunakan tabel.
Dalam mencari nilai KPK dari bilangan kamu dapat menggunakan beberapa metode diantaranya kelipatan persekutuan, faktorisasi prima, dan menggunakan tabel.
1. Kelipatan Persekutuan
Kelipatan persekutuan adalah kelipatan yang sama dari dua bilangan ataupun lebih. KPK adalah nilai terkecil dari kelipatan persekutuan 2 ataupun lebih bilangan.
Contoh: Carilah KPK dari 4 dan 8
Penyelesaian:
Kelipatan 4 adalah = { 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, …}
Kelipatan 8 adalah = {8, 16, 24, 32, 40, 48, 56, …}
Kelipatan persekutuannya adalah 8, 26, 24, 32, … (Kelipatan yang sama dari 4 dan 8)
Nilai yang terkecil adalah 8, sehingga KPK dari 4 dan 8 adalah = 8
2. Faktorisasi Prima
Hal yang dapat kamu lakukan dalam mencari KPK menggunakan cara faktorisasi prima yaitu kamu dapat mengalikan semua bilangan faktor dan apabila ada yang sama ambillah nilai yang paling terbesar, apabila keduanya sama maka ambil salah satunya.
Contoh: Carilah KPK 8, 12, dan 30
Penyelesaian:
Buat pohon faktornya
Faktorisasi prima dari 8 = 2 x 2 x 2 = 2³
Faktorisasi prima dari 12 = 2 x 2 x 3 = 2² x 3
Faktorisasi prima dari 30 = 2 x 3 x 5
- Faktor 2 yang terbesar adalah 2³
- Faktor 3 nilainya sama untuk 12 dan 30 ambil salah satunya saja yaitu 3
- Faktor 5 ada 1 ambil nilai 5
Sehingga dapat diketahui bahwa KPK dari 8, 12, 30 adalah 2³ x 3 x 5 = 120
3. Tabel
Hampir sama dengan mencari FPB, pada hakikatnya cara ini memiliki prinsip yang sama.
Contoh:
a. Tentukan KPK dari bilangan 16 dan 40
16
|
40
| |
2
|
8
|
20
|
2
|
4
|
10
|
2
|
2
|
5
|
2
|
1
|
5
|
5
|
1
|
1
|
KPK = 2 X 2 X 2 X 2 X 5
= 24 X 5 = 80
b. Tentukan KPK dari bilangan 10, 15 dan 25
10
|
15
|
25
| |
2
|
5
|
15
|
25
|
3
|
5
|
5
|
25
|
5
|
1
|
1
|
5
|
5
|
1
|
1
|
1
|
KPK = 2 X 3 X 5 X 5
= 2 X 3 X 52 = 150
Contoh Soal Cerita KPK
Contoh 1: Ali berenang 10 hari sekali, Budi berenang 15 hari sekali, sedangkan Cecep berenang 20 hari sekali. Ketiga-tiganya sama-sama berenang pertama kali pada tanggal 20 februari 2012, nah kapan ketiga-tiganya sama-sama berenang untuk yang kedua kalinya?
Penyelesaian:
Faktorisasi prima dari 10 = 2 x 5
Faktorisasi prima dari 15 = 3 x 5
Faktorisasi prima dari 20 = 2² x 5
KPK dari 10, 15, dan 20 = 2² x 3 x 5 = 60 (alikan semua faktor, faktor yang sama ambil yang paling besar). Jadi mereka akan sama-sama akan berenang setiap 60 hari sekali.
Mereka akan sama-sama berenang untuk yang kedua kalinya pada tanggal 20 Februari + 60 hari = 20 April. Ingatlah bulan Februari pada tahun kabisar adalah 29 hari, untuk tahun bukan kabisar 28 hari (Tahun 2012 adalah tahun kabisat karena habis dibagi dengan 4)
Mereka akan sama-sama berenang untuk yang kedua kalinya pada tanggal 20 Februari + 60 hari = 20 April. Ingatlah bulan Februari pada tahun kabisar adalah 29 hari, untuk tahun bukan kabisar 28 hari (Tahun 2012 adalah tahun kabisat karena habis dibagi dengan 4)
Contoh 2: Bu Aminah memiliki 20 jeruk dan 30 salak, jeruk dan salah akan dimasukkan ke dalam plastik dengan jumlah yang sama.
Pertanyaan:
a. Berapa jumlah plastik yang diperlukan?
b. Berapa banyak jeruk dan salah pada masing-masing plastik?
Penyelesaian:
Faktorisasi prima dari 20 = 2² x 5
Faktorisasi prima dari 30 = 2 x 3 x 5
FPB dari 20 dan 30 = 2 x 5 = 10 (kalikan faktor yang sama, apabila sama ambil yang terkecil).
a. Jumlah plastik yang diperlukan = 10 plastik
b. Jumlah jeruk pada setiap plastik 20/10 = 2 jeruk, jumlah pada salah pada setiap plastik 30/10 = 3 salak.
Contoh 3: Pak Andi mendapat giliran ronda tiap 4 hari sekali. Pak Henri mendapat giliran ronda setiap 6 hari sekali. Sedangkan pak Acay mendapat giliran ronda setiap 8 hari sekali.
Setiap berapa hari mereka akan ronda bersama-sama? Jika mereka ronda bersama-sama pada tanggal 1 Januari 2008, tanggal berapakah mereka ronda bersama-sama lagi?
Setiap berapa hari mereka akan ronda bersama-sama? Jika mereka ronda bersama-sama pada tanggal 1 Januari 2008, tanggal berapakah mereka ronda bersama-sama lagi?
Penyelesaian:
KPK dari 4, 6, dan 8
| 4 | 6 | 8 | |
| 2 | 2 | 3 | 4 |
| 2 | 1 | 3 | 2 |
| 2 | 1 | 3 | 1 |
| 3 | 1 | 1 | 1 |
KPK dari 4, 6, dan 8 = 2 X 2 X 2 X 3
= 23 X 3
= 8 X 3
= 24
Jadi mereka akan beronda secara bersama-sama setiap 24 hari sekali.
FPB = 3
FPB = 2 X 3 X 3= 2 X 32 = 18
FPB = 3 X 5 = 15
Cara Mencari FPB (Faktor Persekutuan Terbesar)
Faktor persekutuan terbesar atau yang biasa disebut seabgai FPB ini merupakan bilangan besar bulat positif yang dapat dibagi habis pada kedua bilangan tersebut.
Ada beberapa metode untuk mencari FPB yaitu, Faktor Persekutuan, Faktorisasi Prima, dan Tabel.
Ada beberapa metode untuk mencari FPB yaitu, Faktor Persekutuan, Faktorisasi Prima, dan Tabel.
1. Faktor Persekutuan
Faktor persekutuan adalah faktor yang sama dari dua bilangan ataupun lebih dan FPB itu sendiri adalah nilai yang paling besar dari faktor persekutuan dua bilangan atau lebih.
Contoh: Carilah FPB dari 4, 8, dan 12
Penyelesaian:
Faktor dari 4 adalah = {1, 2, 4}
Faktor dari 8 adalah = {1 , 2, 4, 8}
Faktor dari 12 adalah = {1, 2, 4, 6, 12}
Faktor persekutuannya adalah 1, 2, 4
Nilai yang terbesar adalah 4, sehingga FPBnya adalah 4
2. Faktorisasi Prima
Pada cara ini kamu dapat mengambil bilangan faktor yang sama, selanjutnya ambil yang terkecil dari 2 atau lebih bilangan.
Contoh:
a. Carilah FPB dari 4, 8, dan 12
Penyelesaian:
Buatlah pohon faktornya,
Faktorisasi prima dari 4 = 2 x 2 = 2²
Faktorisasi prima dari 8 = 2 x 2 x 2 = 2³
Faktorisasi prima dari 12 = 2 x 2 x 3 = 2² x 3
Sehingga faktor dari 4, 8, dan 12 yang sama adalah 2, dan yang terkecil adalah 2²= 4
Maka FPB dari 4, 8, dan 12 adalah 4.
b. Tentukan FPB dari bilangan 20 dan 30
- 2 dan 5 adalah bilangan prima yang sama-sama terdapat dalam faktorisasi prima pada kedua pohon faktor.
- Pangkat terendah dari 2 adalah 1.
- Pangkat terendah dari 5 adalah 1.
- Makan FPB = 2 x 5 = 10
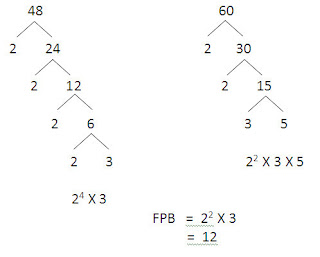
c. Tentukan FPB dari bilangan 48 dan 60
2 dan 3 adalah bilangan prima yang memiliki kesamaan faktorisasi prima dari kedua pohon faktor, dimana pangkat terendah dari kedua adalah 2 dan pangkat terendah dari 3 adalah 1 sehingga FPB dari kedua bilangan tersebut adalah 2² x 3 = 12
3. Tabel
Cara tabel cukup mudah yaitu hanya dengan membagi bilangan yang dicari menggunakan bilangan prima.
a. Tentukan FPB dari bilangan 21 dan 35
21
|
35
| |
3
|
7
|
5
|
5
|
7
|
1
|
7
|
1
|
1
|
FPB = 3
b. Tentukan FPB dari bilangan 36 dan 54
36
|
54
| |
2
|
18
|
27
|
2
|
9
|
27
|
3
|
3
|
9
|
3
|
1
|
3
|
3
|
1
|
1
|
FPB = 2 X 3 X 3= 2 X 32 = 18
Pada contoh a karena bilangan 3 saja yang dapat dibagi habis 21 dan 35 maka FPB = 3.
Pada contoh b hanya diberi huruf tebal yang dapat dibagi habis pada bilangan atasnya saja.
c. Tentukan FPB dari bilangan 75, 105 dan 120
75
|
105
|
120
| |
2
|
75
|
105
|
60
|
2
|
75
|
105
|
30
|
2
|
75
|
105
|
15
|
3
|
25
|
35
|
5
|
5
|
5
|
7
|
1
|
5
|
1
|
7
|
1
|
7
|
1
|
1
|
1
|
FPB = 3 X 5 = 15
Kalkulator KPK dan FPB
Kalkulator Kelipatan Persekutuan terKecil [KPK] dan Faktor Persekutuan terBesar [FPB]
Kalkulator KPK dan FPB
Demikian pembahasan mengenai kpk dan fpb semoga bermanfaat, jika kurang jelas bisa kamu tanyakan di kolom komentar ya.[]