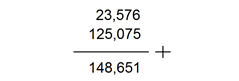✅Pengertian Bilangan Desimal, Operasi dan Pembulatan
Apa itu bilangan desimal dan pecahan desimal? bagaimana cara untuk melakukan operasi hitung pada bilangan desimal itu. Untuk menjawab pertanyaan tersebut, pelajarilah materi ini dengan baik.
A. Pengertian Bilangan Desimal
Bilangan desimal adalah sistem bilangan yang memakai angka berbasis 10 atau sistem bilangan yang menggunakan 10 macam angka yaitu 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Bilangan desimal juga disebut dengan sistem bilangan seper sepuluh.
Dalam definisi lain bilangan desimal adalah bilangan yang merupakan bentuk lain dari bilangan pecahan dengan ciri yaitu terdapat koma pada bilangan tersebut.
B. Bilangan Desimal Menggunakan Nilai Tempat
Berdasarkan definisi yang ada pada sub pembahasan sebelumnya, maka dapat dibuat beberapa contoh bilangan-bilangan desimal antara lain sebagai berikut.
- 0,5
- 0,75
- 0,125
Dari ketiga contoh tersebut, didapati bahwa bilangan desimal memiliki nilai tempat yaitu:
- 0,5 (memiliki satu tempat desimal atau 1 angka di belakang koma)
- 0,75 (memiliki dua tempat desimal atau 2 angka di belakang koma)
- 0,125 (memiliki tiga tempat desimal atau 3 angka di belakang koma)
Nilai-nilai tempat yang dimiliki oleh suatu bilangan desimal tersebut selanjutnya memiliki nilai sendiri-sendiri.
Contoh:
Misalkan dipunya bilangan desimal 123,456 dari bilangan desimal tersebut didapati nilai tempat yaitu sebagai berikut.
- 6 = seperseribuan, nilainya adalah 0,006
- 5 = seperseratus, nilainya adalah 0,05
- 4 = sepersepuluh, nilainya adalah 0,4
- 3 = satuan, nilainya 3
- 2 = puluhan, nilainya 20
- 1 = ratusan, nilainya 100
Apabila nilai-nilai tersebut ditulis dalam bentuk panjang menjadi berikut ini:
123,456 = 100 + 20 + 3 + 0,4 + 0,05 + 0,006
Contoh:
Untuk contoh yang lain, perhatikan contoh bilangan 456,789 berikut ini.
- 9 = seperseribuan, nilainya 0,009
- 8 = seperseratusan, nilainya 0,08
- 7 = sepersepuluh, nilainya 0,7
- 6 = satuan, nilainya 6
- 5 = puluhan, nilainya 50
- 4 = ratusan, nilainya 400
Bilangan tersebut dapat ditulis dalam bentuk panjang menjadi seperti berikut.
456,789 = 400 + 50 + 6 + 0,7 + 0,08 + 0,009
C. Pembulatan Bilangan Desimal
Bilangan desimal merupakan bilangan yang memiliki ciri adanya koma pada bilangan tersebut. Dengan demikian, akan ada bilangan yang memiliki banyak angka setelah koma.
Untuk mempermudah penulisan, maka perlu dilakukan penyederhanaan berupa pembulatan bilangan desimal. Berikut ini disampaikan aturan dalam pembulatan bilangan bulat.
1. Jika angka yang mengalami pembulatan < 5, maka angka tersebut dihilangkan
Misalkan dipunyai sebuah bilangan desimal dengan angka yang akan dibulatkan adalah kurang dari 5.
Apabila kita ingin melakukan pembulatan terhadap bilangan tersebut, maka pembulatan dilakukan dengan menghilangkan angka tersebut.
Untuk lebih jelasnya, perhatikan contoh-contoh pembulatan di bawah ini.
- 1,74 = 1,7 (dibulatkan sampai satu tempat desimal)
- 2,5434 = 2,54 (dibulatkan sampai dua tempat desimal)
- 10,2354 = 10,235 (dibulatkan sampai tiga tempat desimal)
2. Jika angka yang mengalami pembulatan > 5, maka angka di depannya ditambah satu
Misalkan dipunyai sebuah bilangan desimal dengan angka yang akan dibulatkan adalah lebih dari 5.
Apabila kita ingin melakukan pembulatan terhadap bilangan tersebut, maka pembulatan dilakukan dengan angka di depannya di tambah satu.
Untuk lebih jelasnya, perhatikan contoh-contoh pembulatan di bawah ini.
- 2,76 = 2,8 (dibulatkan sampai satu tempat desimal)
- 3,5494 = 3,55 (dibulatkan sampai dua tempat desimal)
- 10,2357 = 10,236 (dibulatkan sampai tiga tempat desimal)
D. Operasi Hitung Bilangan Desimal
Bilangan desimal merupakan bentuk lain dari bilangan pecahan dimana bilangan pecahan adalah bagian dari bilangan rasional.
Dengan demikian, operasi hitung yang berlaku pada bilangan desimal sama seperti bilangan rasional.
Berikut ini akan dijelaskan beberapa operasi hitung pada bilangan desimal beserta tata cara perhitungannya.
1. Penjumlahan Bilangan Desimal
Misalkan dipunyai dua bilangan desimal. Untuk menjumlahkan kedua bilangan desimal tersebut dengan benar dilakukan dengan menjumlahkan angka-angka yang nilai tempatnya sama yaitu sebagai berikut ini.
- ratusan dijumlahkan dengan ratusan
- puluhan dijumlahkan dengan puluhan
- satuan dijumlahkan dengan satuan
- sepersepuluhan dijumlahkan dengan sepersepuluhan
- seperseratusan dijumlahkan dengan seperseratusan
- seperseribuan dijumlahkan dengan seperseribuan
untuk lebih jelasnya, perhatikan contoh di bawah ini.
Contoh:
Tentukan hasil penjumlahan 23,576 + 125,075 !
Jawab:
23,576 + 125,075 = 148,651
Amati kembali contoh 1 di atas. Penjumlahan di atas akan lebih mudah apabila dilakukan dengan cara bersusun dan dengan meluruskan tanda komanya ( , ) seperti berikut ini.
Dengan penjumlahan bersusun seperti gambar di atas, kita lebih mudah dalam menjumlahkan bilangan-bilangan desimal.
2. Pengurangan Bilangan Desimal
Untuk melakukan pengurangan bilangan-bilangan desimal, hal yang kita lakukan sama seperti penjumlahan bilangan desimal yaitu mengurangkan angka-angka yang nilai tempatnya sama.
Untuk lebih jelasnya, perhatikan contoh berikut.
Contoh:
Tentukan hasil pengurangan 24,57 – 18,035 !
Jawab:
24,570 – 18,035 = 6,535
Jika pengurangan tersebut dinyatakan dengan cara bersusun dan dengan meluruskan tanda komanya ( , ) menjadi seperti berikut ini.
Dengan melakukan pengurangan secara bersusun seperti gambar di atas, kita lebih mudah dalam mengurangkan bilangan-bilangan desimal.
3. Perkalian Bilangan Desimal
Perkalian pada bilangan desimal dapat dilakukan dengan dua cara yaitu merubah bilangan desimal menjadi bilangan pecahan terlebih dahulu dan melalui perkalian bertingkat.
Merubah menjadi pecahan biasa
Salah satu cara untuk mengalikan bilangan-bilangan desimal adalah dengan merubah bilangan desimal menjadi pecahan biasa.
Setelah didapati pecahan biasa, barulah dilakukan perkalian pecahan. Untuk lebih jelasnya, pahamilah contoh berikut.
Contoh:
Tentukan hasil perkalian 3,25 x 0,5 !
Jawab:
3,25 x 0,5 = 134 x 12
3,25 x 0,5 = 138
3,25 x 0,5 = 1,625
Jadi hasil perkalian 3,25 x 0,5 = 1,625.
Perkalian bertingkat
Perkalian bertingkat merupakan salah satu cara untuk melakukan perkalian bilangan desimal. Berikut ini adalah contoh perkalian bilangan desimal dengan cara bertingkat.
Tentukan hasil perkalian 3,25 x 0,5 !
Jawab:
Jadi hasil perkalian 3,25 x 0,5 = 1,625.
4. Pembagian Bilangan Desimal
Sama halnya dengan perkalian, pembagian bilangan desimal juga dilakukan dengan dua cara yaitu merubah bilangan desimal menjadi bilangan pecahan terlebih dahulu dan melalui perkalian bertingkat. Berikut dijelaskan dua cara tersebut.
Merubah menjadi pecahan biasa
Merubah bilangan desimal menjadi bentuk pecahan dahulu adalah salah satu cara untuk membagi bilangan desimal.
Berikut ini diberikan contoh pembagian bilangan desimal dengan merubah menjadi pecahan biasa terlebih dahulu.
Contoh:
Tentukan hasil pembagian 3,25 : 0,5 !
3,25 x 0,5 = 134 : 12
3,25 x 0,5 = 134 x 213,25 x 0,5 = 264
3,25 x 0,5 = 6,5
Jadi hasil pembagian 3,25 : 0,5 = 6,5
Pembagian bertingkat
Untuk melakukan pembagian bertingkat, maka kita harus menghilangkan tanda koma pada bilangan desimal dengan mengalikan bilangan-bilangan tersebut dengan bilangan 10n dimana n adalah desimal terbesar.
Untuk lebih jelasnya, perhatikan contoh di bawah ini.
Contoh:
Tentukan hasil pembagian 3,25 : 0,5 !
Jawab:
3,25 memiliki 2 desimal
0,5 memiliki 1 desimal.
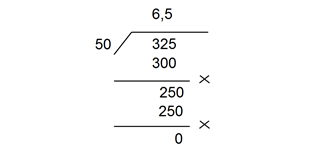
Dengan demikinan nilai n = 2 sehingga masing-masing bilangan dikalikan 100 menjadi:
3,25 x 100 = 325
0,5 x 100 = 50
Selanjutnya:
Jadi hasil pembagian 3,25 : 0,5 = 6,5.