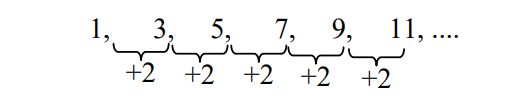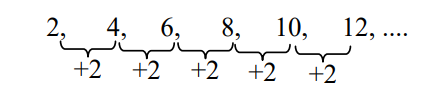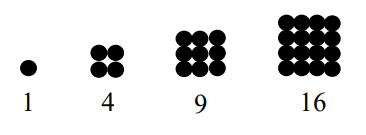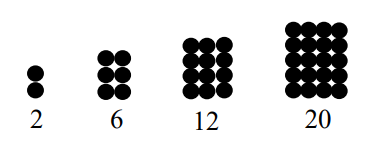Pengertian Pola Bilangan | Macam, Rumus & Contoh
A. Pengertian Pola Bilangan
Pola Bilangan adalah aturan yang digunakan untuk menyusun bilangan-bilangan sehingga menjadi barisan yang teratur dan memiliki suatu pola tertentu.
Perhatikan susunan bilangan di bawah ini.
1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, …
Susunan bilangan di atas adalah contoh susunan bilangan yang memiliki pola bilangan tertentu. Adapun pola yang digunakan adalah bilangan berikutnya diperoleh dengan menambahkan 2 pada bilangan sebelumnya.
Pola bilangan yang membentuk susunan bilangan di atas membuatnya menjadi lebih teratur dan berpola.
Dari definisi di atas, maka dapat disebutkan kembali beberapa contoh susunan bilangan dengan pola tertentu antara lain:
- 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …
- 2, 4, 6, 8, 10, 12, 14, 16, 18, …
- 2, 4, 8, 16, 32, 64, 128, 256, …
- 100, 90, 80, 70, 60, 50, 40, 30, …
B. Macam Macam Pola Bilangan
Susunan bilangan-bilangan memiliki jumlah yang sangat banyak. Dari sekian banyak jumlahnya, tentunya susunan bilangan tersebut memiliki pola-pola tertentu.
Berikut disajikan macam-macam pola bilangan yang biasa ditemui oleh kita.
1. Pola Bilangan Ganjil
Pola bilangan ganjil didefinisikan sebagai aturan yang digunakan untuk menyusun bilangan-bilangan yang beranggotakan bilangan ganjil secara urut.
Untuk lebih jelasnya, perhatikan contoh berikut.
Berikut diberikan contoh barisan yang memiliki pola bilangan ganjil.
1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, …
Dari contoh di atas, maka didapati rumus pola bilangan ganjil adalah sebagai berikut.
Rumus pola bilangan ganjil ke n adalah Un = 2n-1
2. Pola Bilangan Genap
Pola bilangan genap adalah aturan yang digunakan untuk menyusun bilangan-bilangan yang beranggotakan bilangan genap secara urut.
Untuk lebih jelasnya, perhatikan contoh berikut.
Contoh di atas merupakan contoh barisan dengan pola bilangan genap. Hal ini dikarenakan semua bilangan penyusun barisan di atas adalah bilangan genap dimana bilangan berikutnya diperoleh dengan menambahkan bilangan 2 pada bilangan sebelumnya.
Berikut disajikan contoh barisan yang memiliki pola bilangan genap.
2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, …
Dari beberapa contoh di atas, maka didapati rumus pola bilangan genap adalah sebagai berikut.
Rumus pola bilangan genap ke-n adalah Un = 2n
3. Pola Bilangan Persegi
Pola bilangan persegi adalah suatu aturan yang digunakan untuk menyusun bilangan-bilangan dengan membentuk pola persegi.
Untuk lebih jelasnya, perhatikan contoh di bawah ini.
Contoh di atas merupakan contoh barisan dengan pola bilangan persegi. Hal ini dikarenakan semua bilangan penyusun barisan di atas merupakan hasil kuadrat dari suatu bilangan dan bilangan-bilangan tersebut membentuk pola suatu persegi.
Dari penjelasan di atas, maka untuk mendapati susunan bilangan dengan pola persegi dapat digunakan rumus berikut ini.
Rumus pola bilangan persegi ke-n adalah Un = n2
4. Pola Bilangan Persegi Panjang
Pola bilangan persegi panjang adalah aturan untuk menyusun bilangan-bilangan yang mana apabila bilangan-bilangan tersebut diwujudkan dalam suatu objek geometri membentuk pola persegi panjang.
Untuk lebih jelasnya, amatilah contoh di bawah ini.
Contoh di atas merupakan contoh barisan dengan pola bilangan persegi panjang. Hal ini dikarenakan semua bilangan penyusun barisan di atas merupakan bilangan-bilangan yang apabila dinyatakan dalam geometri membentuk pola persegi panjang.
Dari penjelasan di atas, maka untuk mendapati susunan bilangan dengan pola persegi panjang dapat digunakan rumus berikut ini.
Rumus pola bilangan persegi panjang ke-n adalah Un = n x ( n + 1 )
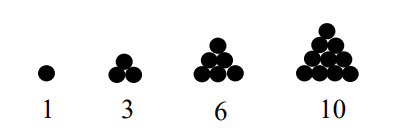
5. Pola Bilangan Segitiga
Pola bilangan segitiga adalah suatu aturan dalam penyusunan bilangan-bilangan dimana dalam penyusunannya membentuk pola berbentuk segitiga. Pola segitiga ini didapat ketika kita mengubah susunan bilangan-bilangan tersebut dalam bentuk geometri.
Untuk lebih jelasnya, perhatikan contoh di bawah ini.
Contoh di atas merupakan contoh barisan dengan pola bilangan segitiga. Hal ini dikarenakan semua bilangan penyusun barisan di atas merupakan bilangan-bilangan yang apabila dinyatakan dalam geometri membentuk pola segitiga.
Dari penjelasan di atas, maka untuk mendapati susunan bilangan dengan pola segitiga dapat digunakan rumus berikut ini.
Rumus pola bilangan segitiga ke-n adalah Un = ½ n (n+1)6. Pola Bilangan Fibonacci
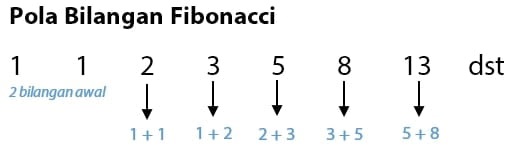
Pola bilangan ini didapat dari penjumlahan dua bilangan sebelumnnya. Rumus suku ke-n pola bilangan Fibonacci adalah:
Un = Un-1 + Un-2
Rumus tersebut berarti suku ke-n merupakan penjumlahan dari dua suku sebelumnya.
Bilangan Fibonacci mempunyai 2 suku utama yaitu 1 dan 1. Suku ke-3 merupakan hasil penjumlahan suku pertama dan kedua, suku ke-4 merupakan hasil penjumlahan suku ketiga dan kedua, demikian seterusnya.
Contoh pola bilangan Fibonacci 1, 1, 2, 3, 5, 8, 13 dan seterusnya.
7. Pola Bilangan Segitiga Pascal
Blaise Pascal seorang matematikawan asal perancis, menyusun pola bilangan yang dapat dibentuk menjadi sebuah segitiga.
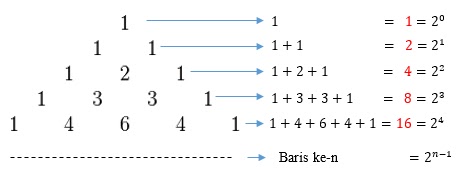
Pola tersebut disebut sebagai pola segitiga pascal.Untuk lebih memahami pola ini perhatikan gambar berikut ini.
Pola bilangan segitiga pascal merupakan jumlah bilangan – bilangan dari setiap baris pada segitiga pascal.
Contoh pada baris ke 3 dari segitiga pascal terdiri atas barisan bilangan 1, 2, dan 1 sehingga bilangan U3 sama dengan 1 + 2 + 1 = 4. Barisan bilangan segitiga pascal adalah 1, 2, 4, 8, 16 dan seterusnya.
Rumus pola bilangan segitiga pascal ke-n adalah Un = 2n-1