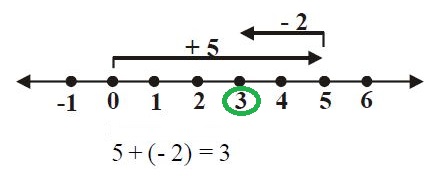Widget HTML Atas

Home / Bilangan / Matematika

Garis Bilangan | Cara Membaca, Contoh Gambar, Operasi & Soal

Oleh Admin

Pengertian Garis Bilangan

Dalam matematika garis bilangan adalah suatu gambar garis lurus di mana tiap titiknya melambangkan suatu bilangan serta setiap bilangan merujuk pada satu titik tertentu yang berjarak sama di sepanjang garis ini.

Garis ini mencakup seluruh bilangan berkelanjutan tak terhingga ke kedua arahnya. Bilangan tersebut bisa berupa bilangan real, bilangan rasional, ataupun bilangan bulat. 

Garis bilangan berfungsi sebagai perlengkapan bantu dalam mengajar penjumlahan serta pengurangan sederhana, khususnya yang melibatkan bilangan negatif.

Contoh Gambar Garis Bilangan

Contoh Gambar Garis Bilangan

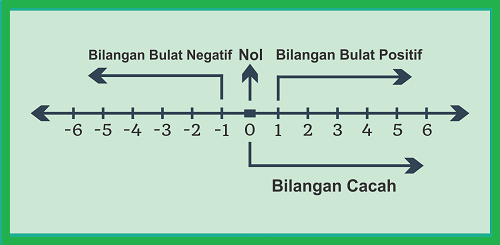
Garis ini dibagi menjadi dua bagian simetri oleh titik nol, yakni titik yang melambangkan angka nol.

Garis Bilangan Bulat

Garis bilangan digunakan untuk memudahkan melakukan perhitungan bilangan bulat untuk operasi hitung penjumlahan dan pengurangan.

Membaca Garis Bilangan Bulat

Garis Bilangan Bulat
Artikel Terkait: Pengertian Bilangan Bulat

Cara membaca garis bilangan bulat diatas adalah sebagai berikut:
  • Arah panah ke kanan menunjukkan bilangan bulat positif
  • Arah panah ke kiri menunjukkan bilangan bulat negatif
  • 5 dibaca lima
  • 4 dibaca empat
  • 3 dibaca tiga
  • 2 dibaca dua
  • 1 dibaca satu
  • 0 dibaca nol
  • -1 dibaca negatif satu
  • -2 dibaca negatif dua
  • -3 dibaca negatif tiga
  • -4 dibaca negatif empat
  • -5 dibaca negatif lima

Menentukan Letak Bilangan Bulat Pada Garis Bilangan

Pada gambar diatas:
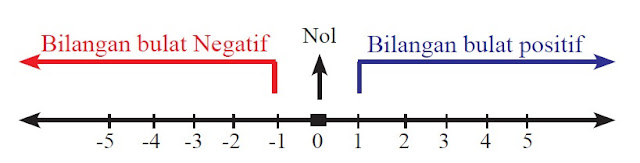
  • Bilangan bulat positif terletak disebelah kanan 0(nol)
  • Bilangan bulat negatif terletak disebelah kiri 0(nol)

Lawan Suatu Bilangan

Perhatikan lagi gambar diatas:
  • Bilangan bulat postitif merupakan lawan bilangan bulat negatif
  • Bilangan bulat negatif merupakan lawan bilangan bulat positif
  • 1 adalah lawan dari -1
  • 2 adalah lawan dari -2
  • 3 adalah lawan dari -3
  • 4 adalah lawan dari -4
  • 5 adalah lawan dari -5

Membandingkan Dua Bilangan Bulat

Perhatikan lagi gambar diatas:

1. Jika sebuah bilangan terletak di sebelah kanan bilangan lain maka nilai bilangan itu lebih besar (>)

Semakin kanan posisi suatu bilangan, semakin besar nilai bilangan tersebut.

Contoh
  • 5 > 4 karena 5 letaknya di sebelah kanan 4
  • -2 > -3 karena -2 letaknya di sebelah kanan -3
  • -3 > -5 karena -3 letaknya di sebelah kanan -5
2. Jika sebuah bilangan terletak di sebelah kiri bilangan lain maka nilai bilangan itu lebih kecil (<)

Semakin kiri posisi suatu bilangan, semakin kecil nilai bilangan tersebut.

Contoh
  • 4 < 5 karena 4 letaknya di sebelah kiri 5
  • -5 < -1 karena -5 letaknya di sebelah kiri -1
  • -4 < -3 karena -4 letaknya di sebelah kiri -3

Mengurutkan Bilangan Bulat

Cara mengurutkan bilangan bulat bisa kamu mulai dari angka terbesar pada bilangan negatif, karena semakin besar angka bilangan negatif, maka semakin kecil nilai bilangan negatif itu.

Bilangan negatif selalu lebih kecil dari bilangan positif dan nol, sebaliknya bilangan positif selalu lebih besar dari bilangan negatif dan nol.

Agar lebih mudah memahami cara mengurutkan bilangan bulat perhatikan contoh di bawah ini.

Urutkan bilangan bulat berikut ini mulai dari yang terkecil dan mulai dari yang terbesar!

1. -4,-1,-3, 8, 7, -5

Jawab

Dari yang terkecil: -5, -4, -3, -1, 7, 8

Dari yang terbesar: 8, 7, -1, -3, -4, -5

2. 9, -5, 6, -12, 17, 8, -14

Jawab

Dari yang terkecil: -14, -12, -5, 6, 8, 9, 17

Dari yang terbesar: 17, 9, 8, 6, -5, -12, -14

Penjumlahan Bilangan Bulat dengan Garis Bilangan

Aturan operasi hitung penjumlahan pada garis bilangan :

  • Titik awal adalah angka nol
  • Penjumlahan tarik garis ke kanan
  • Titik terakhir merupakan hasil perhitungan

Contoh

Selesaikan penjumlahan berikut memakai garis bilangan!

4 + 5 =

Penyelesaian:

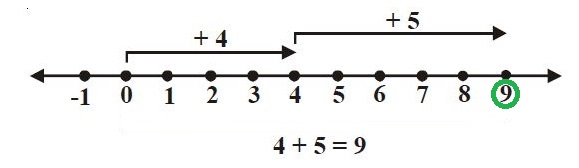
  • Mulai dari titik nol tarik garis empat langkah ke kanan
  • Lalu tarik garis lagi, lima langkah ke kanan
  • Di dapat hasil penjumlahan adalah 9

Penjumlahan Bilangan Bulat dengan Garis Bilangan

Jadi, 4 + 5 = 9

Pengurangan Bilangan Bulat dengan Garis Bilangan

Aturan operasi hitung pengurangan pada garis bilangan :

  • Titik awal adalah angka nol
  • Pengurangan tarik garis ke kiri
  • Titik terakhir merupakan hasil perhitungan
Contoh

Selesaikan pengurangan berikut memakai garis bilangan!

4 - 6 =

Penyelesaian
  • Mulai dari titik nol tarik garis empat langkah ke kanan
  • Lalu tarik garis lagi, enam langkah ke kiri
  • Di dapat hasil penjumlahan adalah -2
Pengurangan Bilangan Bulat dengan Garis Bilangan

Jadi, 4 – 6 = -2

Operasi Hitung Campuran dengan Garis Bilangan

Aturan operasi hitung pada garis bilangan :

  • Titik awal adalah angka nol
  • Penjumlahan tarik garis ke kanan
  • Pengurangan tarik garis ke kiri
  • Titik terakhir merupakan hasil perhitungan

Contoh

Selesaikan operasi berikut memakai garis bilangan!

5 + (–2)

Penyelesaian

  • Mulai dari titik nol tarik garis lima langkah ke kanan
  • Lalu tarik garis lagi, dua langkah ke kiri
  • Di dapat hasil penjumlahan adalah 3

Penjumlahan Bilangan Bulat dengan Garis Bilangan
Jadi, 5 + (–2) = 3



Sekian materi "Garis Bilangan | Cara Membaca, Contoh Gambar, Operasi & Soal". Nantikan materi menarik lainnya dan mohon kesediaannya untuk share . Terima kasih…