√ Rumus Keliling Lingkaran dan Contoh Soalnya Lengkap

Oleh Admin

⭐⭐⭐ Rumus keliling adalah K = 2 × π × r, dengan K = keliling lingkaran, π = konstanta pi (3.14 atau 22/7) dan r = jari-jari lingkaran ⭐⭐⭐

Rumus keliling lingkaran - Untuk menghitung keliling dari sebuah lingkaran sama seperti menghitung tepian lingkaran secara penuh. Pada kesempatan ini kita akan membahas secara detail tentang rumus keliling lingkaran lengkap beserta komponen lingkaran.

Bangun Datar Lingkaran

Apa itu Lingkaran? Lingkaran adalah himpunan titik-titik yang berbentuk lengkungan tertutup dengan jarak sama terhadap satu titik tertentu. Titik tertentu itu disebut dengan Pusat Lingkaran, dan jarak yang sama tersebut disebut dengan jari-jari lingkaran.

lingkaran dan jari-jarinya

Sebuah lingkaran mempunyai Unsur-unsur lingkaran diantaranya adalah:

Titik pusat
Jari-jari
Diameter
Busur
Tali busur
Tembereng
Juring
Apotema
Sudut Pusat
Sudut Keliling

Rumus Keliling Lingkaran

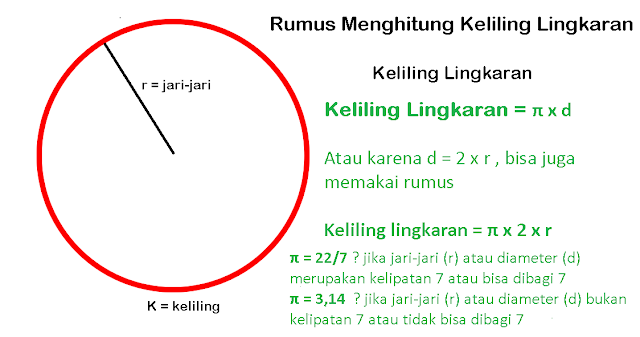
Nah setelah kita mengetahui apa itu lingkaran beserta unsur-unsurnya sekarang saat kita membahas mengenai tema utama yaitu menghitung keliling lingkaran, Untuk cara mencari keliling sebuah lingkaran kita bisa memakai rumus:

Keliling Lingkaran = π x d

Atau karena d = 2 x r , bisa juga memakai rumus

Keliling lingkaran = π x 2 x r

Keterangan:
d merupakan diameter
r merupakan jari-jari
π = 22/7 atau 3.14
Nilai π = 22/7 jika jari-jari(r) atau diameter(d) merupakan kelipatan dari 7 atau bisa dibagi 7
Nilai π = 3,14 jika jari-jari(r) atau diameter(d) bukan kelipatan dari 7 atau tidak bisa dibagi 7

Kedua rumus diatas serupa dan kamu akan mendapatkan hasil yang sama jika menghitung memakai kedua rumus tersebut, kalau tidak percaya boleh kamu coba sendiri.

Contoh Soal Keliling Lingkaran

Agar kamu lebih paham tentang pembahasan ini kamu bisa melihat contoh soal dibawah ini:

Menghitung Keliling Lingkaran Jika Diketahui Jari-jarinya

Contoh Soal:
Soal: Sebuah lingkaran memiliki jari-jari 14 cm. Berapakah keliling lingkaran tersebut?
( Petunjuk: K = π x 2 x r )

jawab:
Keliling = π x 2 x jari-jari
Keliling = 22/7 x 2 x 14
K = 88 cm

Menghitung Keliling Lingkaran Jika diketahui diameternya

Contoh Soal:
Soal: Berapakan keliling suatu lingkaran yang memiliki diameter 6 m?
( Petunjuk: K = π x d )

jawab:

keliling = π x d
K = 22/7 x 6
K = 18,85 m

Baca juga artikel : Rumus luas lingkaran

Menghitung Keliling Lingkaran Jika Diketahui Luasnya

Contoh Soal:
Soal: Sebuah lingkaran mempunyai luas 1256 cm2 hitunglah keliling dari lingkaran itu ?

Jawab:
Luas lingkaran = π r² ⇔ 1256 = 3,14 x r²
r² = 1256/3,14
r² = 400
r = √400
r = 20 cm

keliling = 2 π r
= 2 . 3,14 . 20
= 125,6 cm

Jadi Keliling lingkaran tersebut adalah 125,6cm.

Rumus Keliling Setengah Lingkaran

Untuk mengetahui keliling setengah lingkaran, carilah terlebih dahulu keliling penuh dari lingkaran tersebut, kemudian bagi dua hasilnya. Untuk lebih jelasnya silahkan anda lihat penjelasan di artikel ini.

Contoh Soal Keliling Lingkaran

Contoh Soal 1:
Soal: Jika ada sebuah kolam renang berbentuk lingkaran yang mempunyai diameter 20 m. Jika seseorang berlari mengelilingi kolam tersebut 12 kali, berapakah jarak yang ia tempuh ?

Jawab:
jarak yang ditempuh adalah = 12 x keliling kolam
= 12 x π x d
= 12 x 3,14 x 20
= 753,6 m

Contoh Soal 2:
Soal: Jika sebuah motor mempunyai roda dengan jari-jari 42 cm berputar sebanyak 2000 kali, berapah jarak yang di tempuh oleh motor tersebut ?

Jawab:
jarak yang ditempuh motor sama dengan 2000 kali keliling lingkaran ( roda )
maka jarak yang ditempuh motor = 1000 x π x d = 1.000 x 22/7 x 84 cm = 264000 cm = 2,64 km.

Baca juga tutorial lainnya : Daftar Materi Pelajaran Matematika

Demikianlah penjelasan lengkap tentang rumus keliling lingkaran dan contoh soal. Semoga bermanfaat dan mohon bantuannya untuk share artikel ini ya.

Referensi:
Radius, diameter, & circumference