√ Pengertian Lingkaran dan Bagian-bagiannya Lengkap

A. Pengertian Lingkaran

Pengertian Lingkaran adalah kedudukan titik-titik yang berjarak sama terhadap suatu titik tertentu. Jarak yang sama tersebut di sebut dengan jari jari lingkaran dan titik titik tertentu di sebut pusat lingkaran.

Dalam sebuah pengertian lain, Definisi lingkaran yang menyatakan bahwa lingkaran adalah sebuah garis lengkung yang bertemu kedua ujungnya dan semua titik letaknya sama jauh dari sebuah titik tertentu. Titik ini di sebut pusat lingkaran, garis lengkung yang bertemu kedua ujungnya itu disebut dengan keliling lingkaran sedangkan jarak dari suatu titik pada lingkaran ke titik pusat disebut dengan jari-jari lingkaran . Daerah yang dibatasi oleh lingkaran dinamakan bidang lingkaran.

B. Bagian-bagian Lingkaran

Perhatikan gambar dibawah ini.

Pada gambar pertama titik P disebut titik pusat lingkaran dan garis R disebut jari-jari. Dan pada gambar nomor dua garis TB di sebut tali busur lingkaran dan garis D disebut diameter lingkaran.

Pada gambar ketiga dari atas Panjang garis lengkung yang tercetak tebal yang berbentuk lingkaran disebut keliling lingkaran, sedangkan daerah yang di arsir di dalamnya di sebut bidang lingkaran atau luas lingkaran.

Pada gambar nomor empat Daerah T yang diarsir disebut dengan tembereng dan daerah J yang diarsir disebut Juring.

Dari penjelasan diatas jika dirangkum lebih rinci maka bagian-bagian lingkaran antara lain:

1. Jari-jari Lingkaran
2. Titik Pusat Lingkaran
3. Busur Lingkaran
4. Diameter Lingkaran
5. Keliling Lingkaran
6. Tembereng Lingkaran
7. Tali Busur Lingkaran
8. Apotema Lingkaran
9. Juring Lingkaran
10. Sudut Keliling Lingkaran
11. Sudut Pusat Lingkaran

Untuk lebih jelas memahami bagian-bagian lingkaran seperti juring dan tembereng kamu dapat membaca tulisan saya sebelumnya di Bagian-bagian/Unsur-unsur Lingkaran Dan Penjelasannya.

C. Sifat-sifat Lingkaran

Lingkaran mempunyai sifat-sifat sebagai berikut:

1. Memiliki satu titik pusat.   
2. Memiliki satu buah sisi.
3. Tidak memiliki titik sudut.
4. Jumlah sudutnya adalah 360º
5. Memiliki simetri lipat dan sumbunya takterhingga
6. Memiliki simetri putar yang tak terhingga

Baca juga: Rumus Bangun Datar

D. Nilai Phi(π)

Phi adalah suatu konstanta(suatu nilai tetap) dalam matematika yang merupakan sifat khusus dari lingkaran, Nilai phi sendiri merupakan nilai perbandingan dari keliling (K) lingkaran dengan diameternya (d) yaitu:

π = (keliling lingkaran) : (diameter lingkaran)

Nilai π dalam 10 tempat desimal adalah 3,1415926535 ( dibulatkan menjadi 3,14 ). Banyak rumus dalam matematika dan sains yang memakai π, yang menjadikannya salah satu dari suatu nilai tetap matematika yang penting. 

π merupakan bilangan irasional, artinya nilai π tidak bisa dinyatakan dalam pembagian bilangan bulat (umumnya pecahan 22/7 dipakai sebagai nilai paling dekat π; tetapi sebetulnya tidak ada satupun pecahan yang bisa mewakili nilai yang sama persis dengan π.)

Agar penggunaan nilai phi (π) lebih mudah dalam perhitungan manual, maka dipakai nilai 22/7 untuk jari-jari lingkaran kelipatan 7 dan nilai 3.14 untuk jari-jari lingkaran bukan kelipatan 7.

E. Keliling Lingkaran

Pengertian keliling lingkaran adalah panjang garis lengkung dari suatu lingkaran. Sekarang perhatikan persamaan nilai phi diatas. Dari persamaan diatas, bisa sobat ketahui jika rumus keliling lingkaran sama dengan phi dikalikan dengan diameter lingkaran.

Rumus keliling lingkaran: K = π.d atau K = 2.π.r

Keterangan:

K : keliling lingkaran

π : phi, konstanta dengan nilai 3,14.. atau 22/7

d : diameter lingkaran

r  : jari-jari lingkaran

F. Luas Lingkaran

Pengertian luas lingkaran adalah luas area yang dibatasi oleh busur lingkaran atau keliling lingkaran. Luas lingkaran bisa kita hitung dengan memakai rumus di bawah ini:

Luas lingkaran: L = π × r²

Keterangan:

L : luas lingkaran

π : phi, konstanta dengan nilai 3,14.. atau 22/7

d : diameter lingkaran

r  : jari-jari lingkaran

Satuan untuk luas lingkaran yang dipakai adalah satuan panjang pangkat dua atau persegi contohnya: centimeter persegi (cm²), milimeter pesersegi (m²) dan lain sebagainya.

Pembuktian Rumus Lingkaran dengan Menurunkan dari Rumus Luas Persegi Panjang

Perhatikan gambar berikut!!

Luas lingkaran bisa ditemukan dengan memotong-motong lingkaran sebagai juring untuk selanjutnya ditata ulang menjadi sebuah persegi panjang yang luasnya bisa dihitung dengan mudah.

Dari gambar diatas kita bisa memperoleh data sebagai berikut:

1. Lingkaran dipotong menjadi 18 buah juring

2. 18 juring disusun menjadi persegi panjang

3. Panjang persegi panjang ( p ) = 9 busur juring = ½ keliling lingkaran = ½ ( 2.π.r )

4. Lebar persegi panjang ( l ) = jari-jari juring = jari-jari lingkaran = r

Maka kita bisa menghitung luas persegi panjang diatas:

Luas persegi panjang = panjang (p) x lebar (l)

Luas persegi panjang = ½ keliling lingkaran x jari-jari lingkaran

Luas persegi panjang = ½ ( 2.π.r ) x r

Luas persegi panjang = π x r x r

Luas persegi panjang = π x r²

Luas persegi panjang = Luas lingkaran

Pembuktian Rumus Lingkaran dengan Menurunkan dari Rumus Luas Jajar Genjang

Selain disusun menjadi sebuah persegi panjang, Luas lingkaran bisa ditemukan juga dengan memotong-motong lingkaran sebagai juring untuk selanjutnya ditata ulang menjadi jajar genjang. Sehingga luas lingkaran bisa kita hitung memakai rumus luas jajar genjang. 

Dari gambar diatas kita bisa memperoleh data sebagai berikut:

1. Lingkaran dipotong menjadi 12 buah juring

2. 12 juring disusun menjadi jajar genjang

3. Alas jajar genjang ( a ) = 6 busur juring = ½ keliling lingkaran = ½ ( 2.π.r )

4. Tinggi jajar genjang ( t ) = jari-jari juring = jari-jari lingkaran = r

Maka kita bisa menghitung luas jajar genjang diatas:

Luas jajar genjang = alas (a) x tinggi (t)

Luas jajar genjang = ½ keliling lingkaran x jari-jari lingkaran

Luas jajar genjang = ½ ( 2.π.r ) x r

Luas jajar genjang = π x r x r

Luas jajar genjang = π x r²

Luas jajar genjang = Luas lingkaran

 G. Busur

Busur dalam lingkaran adalah garis lengkung yang jadi bagian dari keliling lingkaran. Busur dibagi jadi 2 yakni busur kecil serta busur besar. Disebut busur kecil bila panjangnya kurang dari separuh lingkaran serta disebut busur besar bila panjangnya lebih dari separuh lingkaran.

Penjelasan tentang gambar diatas:

• Garis AB adalah busur lingkaran
• aº adalah besar sudut juring
• OA dan OB adalah jari-jari lingkaran
• Daerah warna biru merupakan luas juring, yakni daerah yang dibatasi oleh dua jari-jari dan sebuah busur.

Sedangkan rumus untuk mencari panjang busur adalah...

H. Panjang Busur, Luas Juring, dan Luas Tembereng

Secara berurutan panjang busur, luas juring dan luas tembereng yang terbentuk oleh dua jari-jari dan sudut pusat lingkaran bisa kita hitung memakai rumus berikut ini.

Panjang Busur

Luas Juring

Luas Tembereng

I. Sudut Pusat dan Sudut Keliling Lingkaran

Pengertian Sudut Pusat dan Sudut Keliling

Sudut pusat lingkaran adalah sudut yang dibentuk oleh dua jari-jari lingkaran yang berpotongan di titik pusatnya. Perhatikan gambar berikut ini agar lebih jelas mengetahui dimana letak sudut pusat.

Keterangan:

        ∠ AOB adalah sudut pusat yang menghadap busur AB.

        ∠ COD adalah sudut pusat yang menghadap busur CD.

Sedangkan sudut keliling adalah sudut yang dibentuk oleh dua tali busur yang berpotongan di satu titik pada keliling lingkaran. Perhatikan gambar berikut ini agar lebih jelas mengetahui dimana letak sudut keliling.

Keterangan:

        ∠ BCA adalah sudut pusat yang menghadap busur AB.

        ∠ XZY adalah sudut pusat yang menghadap busur XY.

Hubungan Sudut Pusat dan Sudut Keliling

1. Sudut keliling dan sudut pusat yang menghadap busur yang sama

Perhatikan gambar dibawah ini!

Besar sudut pusat adalah dua kali besar sudut keliling yang menghadap busur yang sama.

∠ AOB = 2 x ∠ ACB

Besar sudut keliling adalah setengah dari besar sudut pusat yang menghadap busur yang sama.

∠ ACB = ½ x ∠ AOB

2. Sudut keliling yang menghadap busur yang sama

Perhatikan gambar dibawah ini!

Besar sudut keliling yang menghadap busur yang sama adalah sama.

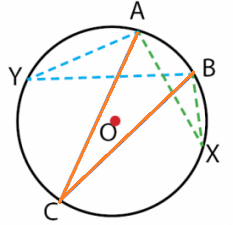
Perhatikan ∠ ACB, ∠ AXB, dan ∠ AYB! Ketiga sudut tersebut menghadap busur yang sama, yaitu busur AB. Maka ukuran besar ketiga sudut tersebut adalah sama yaitu ∠ ACB =∠ AXB = ∠ AYB.

3. Sudut keliling yang saling berhadapan

Perhatikan gambar di bawah ini!

Jumlah dari dua sudut keliling yang saling berhadapan adalah 180º.

Hubungan antara dua sudut keliling ∠ ADC dan ∠ ABC adalah

  ∠ ADC + ∠ ABC = 180º

4. Besar Sudut keliling yang menghadap diamerter lingkaran

Perhatikan gambar di bawah ini!

Besar sudut keliling yang menghadap diameter lingkaran adalah 90º (sudut siku-siku).

  ∠ ADC = ∠ ACB = 90º

5. Segi Empat Tali Busur (Segi empat sudut keliling)

Perhatikan gambar di bawah ini!

∠ ADC + ∠ ABC = 180º

∠ DAB + ∠ DCB = 180º

Sifat-sifat Segi Empat Tali Busur:

• Jumlah dua sudut yang saling berhadapan pada segiempat tali busur adalah 180º.
• Jika sebuah segi empat tali busur salah satu diagonalnya adalah diameter lingkaran disebut dengan segi empat tali busur siku-siku.
• Jika sebuah segi empat tali busur kedua diagonalnya adalah diameter lingkaran maka akan membentuk bangun persegi panjang.
• Jika segi empat tali busur kedua diagonalnya merupakan diameter lingkaran yang saling berpotongan dan tegak lurus maka akan membentuk persegi.

J. Sudut Antara Dua Tali Busur

Sudut Antara Dua Tali Busur yang Berpotongan di dalam Lingkaran

Perhatikan gambar berikut ini!

Lingkaran diatas titik pusatnya adalah O dengan titik E adalah titik potong antara tali busur AC dan BD. Dari gambar diatas dapat dilihat jika ∠ AEB , ∠ BEC, ∠ CED, dan ∠ AED adalah sudut didalam lingkaran yang terbentuk oleh perpotongan tali busur AC dan BD.

Cara mencari besar sudut antara dua tali busur berpotongan di dalam lingkaran:

∠ BEC = ½ ( ∠ BOC + ∠ AOD )

∠ AED = ½ ( ∠ BOC +  ∠ AOD )

∠ CED = ½ ( ∠ AOB + ∠ COD )

∠ AEB = ½ ( ∠ AOB + ∠ COD )

Dari pembahasan diatas bisa kita simpulkan sebagai berikut. Besar sudut antara dua tali busur yang berpotongan didalam lingkaran sama dengan setengah dari jumlah sudut-sudut pusat yang menghadap busur yang diapit oleh kaki-kaki sudut itu.

Sudut Antara Dua Tali Busur yang Berpotongan di luar Lingkaran

Perhatikan gambar dibawah ini!

Titik O merupakan titik pusat lingkaran, sedangkan LK dan MN merupakan dua tali busur yang jika diperpanjang akan berpotongan di titik P. Perpotongan dua tali busur yang ada di titik P dan berada di luar lingkaran membentuk ∠ KPN.

Cara mencari besar sudut antara dua tali busur berpotongan di luar lingkaran:

∠ KPN = ½ ( ∠ MOL - ∠ KON )

---

Baca juga tutorial lainnya : Daftar Materi Pelajaran Matematika

---

Demikian pembahasan singkat tentang apa itu lingkaran dan pengertian lingkaran dan cara menghitung unsur-unsur lingkaran. Nantikan artikel menarik lainnya di rumusmatematika.org, semoga bermanfaat.